题目
1、已知 P(A)=0.5 , P(B)=0.6 , (B|A)=0.8, 则 P(B-A)= __
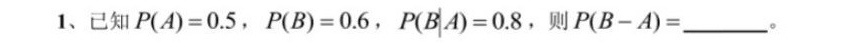
题目解答
答案

解析
步骤 1:确定条件概率公式
根据条件概率的定义,$P(B|A)$ 表示在事件 A 发生的条件下,事件 B 发生的概率。其公式为 $P(B|A) = \frac{P(AB)}{P(A)}$,其中 $P(AB)$ 表示事件 A 和事件 B 同时发生的概率。
步骤 2:计算 $P(AB)$
根据题目给出的条件,$P(B|A) = 0.8$,$P(A) = 0.5$,代入条件概率公式,得到 $0.8 = \frac{P(AB)}{0.5}$。解这个方程,得到 $P(AB) = 0.8 \times 0.5 = 0.4$。
步骤 3:计算 $P(B-A)$
根据概率的加法公式,$P(B-A) = P(B) - P(AB)$。代入题目给出的 $P(B) = 0.6$ 和步骤 2 中计算出的 $P(AB) = 0.4$,得到 $P(B-A) = 0.6 - 0.4 = 0.2$。
根据条件概率的定义,$P(B|A)$ 表示在事件 A 发生的条件下,事件 B 发生的概率。其公式为 $P(B|A) = \frac{P(AB)}{P(A)}$,其中 $P(AB)$ 表示事件 A 和事件 B 同时发生的概率。
步骤 2:计算 $P(AB)$
根据题目给出的条件,$P(B|A) = 0.8$,$P(A) = 0.5$,代入条件概率公式,得到 $0.8 = \frac{P(AB)}{0.5}$。解这个方程,得到 $P(AB) = 0.8 \times 0.5 = 0.4$。
步骤 3:计算 $P(B-A)$
根据概率的加法公式,$P(B-A) = P(B) - P(AB)$。代入题目给出的 $P(B) = 0.6$ 和步骤 2 中计算出的 $P(AB) = 0.4$,得到 $P(B-A) = 0.6 - 0.4 = 0.2$。