题目
[例6] 设函数 (x)=dfrac (x)(a+{e)^bx} 在 (-infty ,+infty ) 内连续,且 lim _(xarrow infty )f(x)=0, 则常数a,b-|||-满足 () .-|||-(A) lt 0 lt 0 (B) gt 0, gt 0-|||-(C) leqslant 0, gt 0 (D) geqslant 0, lt 0

题目解答
答案
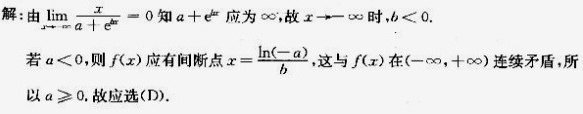
解析
步骤 1:分析极限条件
由题意知 $\lim _{x\rightarrow \infty }f(x)=0$,即 $\lim _{x\rightarrow \infty }\dfrac {x}{a+{e}^{bx}}=0$。这意味着当 $x$ 趋于无穷大时,分母 $a+{e}^{bx}$ 必须趋于无穷大,否则极限不会为0。因此,$b$ 必须小于0,以保证 ${e}^{bx}$ 趋于0,从而 $a+{e}^{bx}$ 趋于 $a$。
步骤 2:分析连续性条件
函数 $f(x)=\dfrac {x}{a+{e}^{bx}}$ 在 $(-\infty ,+\infty )$ 内连续,这意味着分母 $a+{e}^{bx}$ 在整个实数范围内不能为0。如果 $a<0$,则存在某个 $x$ 使得 $a+{e}^{bx}=0$,这会导致函数在该点不连续。因此,$a$ 必须大于等于0。
步骤 3:综合分析
结合步骤1和步骤2的分析,可以得出结论:$a\geqslant 0$ 且 $b\lt 0$。
由题意知 $\lim _{x\rightarrow \infty }f(x)=0$,即 $\lim _{x\rightarrow \infty }\dfrac {x}{a+{e}^{bx}}=0$。这意味着当 $x$ 趋于无穷大时,分母 $a+{e}^{bx}$ 必须趋于无穷大,否则极限不会为0。因此,$b$ 必须小于0,以保证 ${e}^{bx}$ 趋于0,从而 $a+{e}^{bx}$ 趋于 $a$。
步骤 2:分析连续性条件
函数 $f(x)=\dfrac {x}{a+{e}^{bx}}$ 在 $(-\infty ,+\infty )$ 内连续,这意味着分母 $a+{e}^{bx}$ 在整个实数范围内不能为0。如果 $a<0$,则存在某个 $x$ 使得 $a+{e}^{bx}=0$,这会导致函数在该点不连续。因此,$a$ 必须大于等于0。
步骤 3:综合分析
结合步骤1和步骤2的分析,可以得出结论:$a\geqslant 0$ 且 $b\lt 0$。