题目
11.设随机变量 sim P(lambda ) ,已知 X=1 =P X=2 ,求 X=4 -
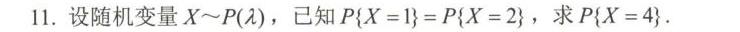
题目解答
答案
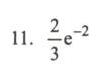
解析
考查要点:本题主要考查泊松分布的概率公式及其应用,以及通过已知条件求解参数λ的能力。
解题核心思路:
- 利用泊松分布的概率公式,根据题目给出的条件$P\{X=1\}=P\{X=2\}$,建立方程求解参数$\lambda$。
- 代入求得的$\lambda$值,计算$P\{X=4\}$的具体表达式。
破题关键点:
- 正确写出泊松分布的概率公式:$P\{X=k\} = \dfrac{\lambda^k e^{-\lambda}}{k!}$。
- **通过等式$\dfrac{\lambda e^{-\lambda}}{1!} = \dfrac{\lambda^2 e^{-\lambda}}{2!}$消去公共因子,解出$\lambda$的值。
- 注意$\lambda > 0$的隐含条件,排除无效解。
步骤1:写出泊松分布的概率公式
泊松分布的概率质量函数为:
$P\{X=k\} = \dfrac{\lambda^k e^{-\lambda}}{k!}, \quad k=0,1,2,\dots$
步骤2:根据条件建立方程
题目给出$P\{X=1\} = P\{X=2\}$,代入公式得:
$\dfrac{\lambda e^{-\lambda}}{1!} = \dfrac{\lambda^2 e^{-\lambda}}{2!}$
步骤3:化简方程求解$\lambda$
两边同时约去$e^{-\lambda}$,得到:
$\lambda = \dfrac{\lambda^2}{2}$
整理为:
$\lambda^2 - 2\lambda = 0 \implies \lambda(\lambda - 2) = 0$
解得$\lambda = 0$或$\lambda = 2$。由于泊松分布的参数$\lambda > 0$,故$\lambda = 2$。
步骤4:计算$P\{X=4\}$
将$\lambda = 2$代入公式:
$P\{X=4\} = \dfrac{2^4 e^{-2}}{4!} = \dfrac{16 e^{-2}}{24} = \dfrac{2}{3} e^{-2}$