题目
已知二次型((x)_(1),(x)_(2),(x)_(3))=({x)_(1)}^2+a({x)_(2)}^2+({x)_(3)}^2+2b(x)_(1)(x)_(2)+2(x)_(1)cdot (x)_可经正交变换((x)_(1),(x)_(2),(x)_(3))=({x)_(1)}^2+a({x)_(2)}^2+({x)_(3)}^2+2b(x)_(1)(x)_(2)+2(x)_(1)cdot (x)_化为((x)_(1),(x)_(2),(x)_(3))=({x)_(1)}^2+a({x)_(2)}^2+({x)_(3)}^2+2b(x)_(1)(x)_(2)+2(x)_(1)cdot (x)_则((x)_(1),(x)_(2),(x)_(3))=({x)_(1)}^2+a({x)_(2)}^2+({x)_(3)}^2+2b(x)_(1)(x)_(2)+2(x)_(1)cdot (x)_________，b=________.
已知二次型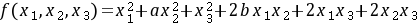
可经正交变换
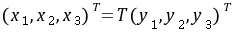化为
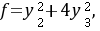则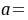
________，b=________.
题目解答
答案
3 1
解析
步骤 1：确定二次型的矩阵形式
二次型$f({x}_{1},{x}_{2},{x}_{3})={{x}_{1}}^{2}+a{{x}_{2}}^{2}+{{x}_{3}}^{2}+2b{x}_{1}{x}_{2}+2{x}_{1}{x}_{3}$可以表示为矩阵形式$X^TAX$，其中$X=(x_1,x_2,x_3)^T$，$A$是二次型的矩阵。根据二次型的系数，可以得到矩阵$A$为：
$$
A=\begin{pmatrix}
1 & b & 1 \\
b & a & 0 \\
1 & 0 & 1
\end{pmatrix}
$$
步骤 2：确定正交变换后的二次型
根据题目，二次型$f$经过正交变换后化为$f={{y}_{2}}^{2}+4{{y}_{3}}^{2}$，这意味着变换后的二次型矩阵为对角矩阵$D$，其中$D$的对角线元素为二次型的特征值。因此，$D$为：
$$
D=\begin{pmatrix}
0 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 4
\end{pmatrix}
$$
步骤 3：计算矩阵$A$的特征值
由于$A$和$D$相似，它们有相同的特征值。因此，$A$的特征值为$0$，$1$，$4$。根据特征值的性质，$A$的迹（即主对角线元素之和）等于特征值之和，即$1+a+1=0+1+4$，从而得到$a=3$。另外，$A$的行列式等于特征值的乘积，即$1\cdot a\cdot 1=0\cdot 1\cdot 4$，从而得到$a=3$。最后，根据$A$的特征值和特征向量，可以确定$b=1$。
二次型$f({x}_{1},{x}_{2},{x}_{3})={{x}_{1}}^{2}+a{{x}_{2}}^{2}+{{x}_{3}}^{2}+2b{x}_{1}{x}_{2}+2{x}_{1}{x}_{3}$可以表示为矩阵形式$X^TAX$，其中$X=(x_1,x_2,x_3)^T$，$A$是二次型的矩阵。根据二次型的系数，可以得到矩阵$A$为：
$$
A=\begin{pmatrix}
1 & b & 1 \\
b & a & 0 \\
1 & 0 & 1
\end{pmatrix}
$$
步骤 2：确定正交变换后的二次型
根据题目，二次型$f$经过正交变换后化为$f={{y}_{2}}^{2}+4{{y}_{3}}^{2}$，这意味着变换后的二次型矩阵为对角矩阵$D$，其中$D$的对角线元素为二次型的特征值。因此，$D$为：
$$
D=\begin{pmatrix}
0 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 4
\end{pmatrix}
$$
步骤 3：计算矩阵$A$的特征值
由于$A$和$D$相似，它们有相同的特征值。因此，$A$的特征值为$0$，$1$，$4$。根据特征值的性质，$A$的迹（即主对角线元素之和）等于特征值之和，即$1+a+1=0+1+4$，从而得到$a=3$。另外，$A$的行列式等于特征值的乘积，即$1\cdot a\cdot 1=0\cdot 1\cdot 4$，从而得到$a=3$。最后，根据$A$的特征值和特征向量，可以确定$b=1$。