题目
当。时,下列函数与。是等价无穷小的是。
当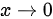 时,下列函数与
时,下列函数与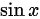 是等价无穷小的是
是等价无穷小的是
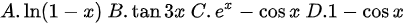
题目解答
答案
解:
根据等价无穷小的替换,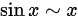
A选项,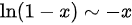 ,不是x的等价无穷小;
,不是x的等价无穷小;
B选项,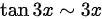 ,不是x的等价无穷小;
,不是x的等价无穷小;
C选项,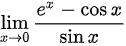 是
是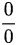 型未定式,根据洛必达法则,对分子分母分别同时求导
型未定式,根据洛必达法则,对分子分母分别同时求导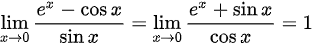 ,是x的等价无穷小;
,是x的等价无穷小;
D选项,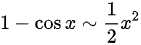 ,不是x的等价无穷小
,不是x的等价无穷小
故答案选C
解析
考查要点:本题主要考查等价无穷小的判断,需要掌握常见函数在$x \to 0$时的泰勒展开式或等价无穷小替换规则,并能灵活运用洛必达法则处理未定式。
解题核心思路:
- 等价无穷小定义:若$\lim_{x \to 0} \frac{f(x)}{\sin x} = 1$,则$f(x)$与$\sin x$是等价无穷小。
- 逐项分析:对每个选项,通过泰勒展开或洛必达法则计算极限,判断是否满足条件。
- 关键点:
- 泰勒展开快速判断低阶项;
- 洛必达法则处理$\frac{0}{0}$型未定式。
选项分析
A. $\ln(1-x)$
- 泰勒展开:$\ln(1-x) \sim -x - \frac{x^2}{2} - \cdots$
- 比较:$\lim_{x \to 0} \frac{\ln(1-x)}{\sin x} = \lim_{x \to 0} \frac{-x}{x} = -1 \neq 1$
- 结论:不是等价无穷小。
B. $\tan 3x$
- 泰勒展开:$\tan 3x \sim 3x + \frac{(3x)^3}{3} + \cdots$
- 比较:$\lim_{x \to 0} \frac{\tan 3x}{\sin x} = \lim_{x \to 0} \frac{3x}{x} = 3 \neq 1$
- 结论:不是等价无穷小。
C. $e^x - \cos x$
- 泰勒展开:
$e^x \sim 1 + x + \frac{x^2}{2}$,$\cos x \sim 1 - \frac{x^2}{2}$
$\Rightarrow e^x - \cos x \sim x + x^2$ - 极限计算:
$\lim_{x \to 0} \frac{e^x - \cos x}{\sin x} = \lim_{x \to 0} \frac{x + x^2}{x} = 1$ - 洛必达验证:
$\lim_{x \to 0} \frac{e^x - \cos x}{\sin x} = \lim_{x \to 0} \frac{e^x + \sin x}{\cos x} = \frac{1 + 0}{1} = 1$ - 结论:是等价无穷小。
D. $1 - \cos x$
- 泰勒展开:$1 - \cos x \sim \frac{x^2}{2}$
- 比较:$\lim_{x \to 0} \frac{1 - \cos x}{\sin x} = \lim_{x \to 0} \frac{\frac{x^2}{2}}{x} = 0 \neq 1$
- 结论:不是等价无穷小。