题目
设二维随机变量((X)^6X)的分布律为((X)^6X)求 ( 1 ) ( X , Y ) 别关于 X Y 的边缘分布律 ; ( 2 ) D ( X ) ; ( 3 )((X)^6X)
设二维随机变量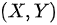 的分布律为
的分布律为
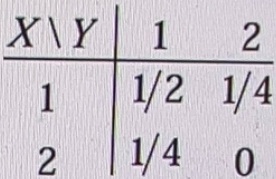
求 ( 1 ) ( X , Y ) 别关于 X Y 的边缘分布律 ;
( 2 ) D ( X ) ;
( 3 )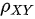
题目解答
答案
解:
(1)X的边缘分布律 :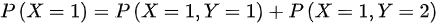
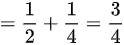
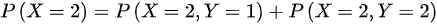
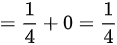
Y的边缘分布律:
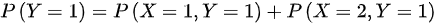
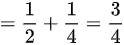
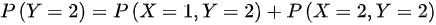
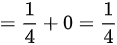
(2)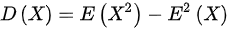
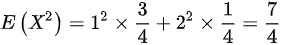
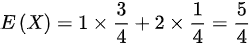
∴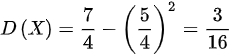
(3)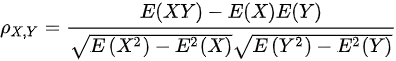
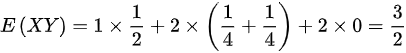
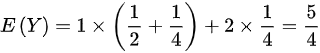
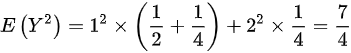
∴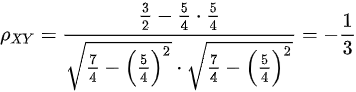
∴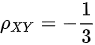
解析
考查要点:
- 边缘分布律的计算:通过联合分布律求解单一变量的分布。
- 方差的计算:利用期望公式展开。
- 相关系数的计算:掌握协方差与标准差的关系。
解题核心思路:
- 边缘分布律:对联合分布律中另一变量的所有可能取值求和。
- 方差:先求期望$E(X)$和$E(X^2)$,再代入公式$D(X)=E(X^2)-[E(X)]^2$。
- 相关系数:通过协方差与标准差的比值计算,注意公式中分子为$E(XY)-E(X)E(Y)$,分母为标准差乘积。
(1)求边缘分布律
X的边缘分布律:
- $P(X=1) = P(X=1,Y=1) + P(X=1,Y=2) = \dfrac{1}{2} + \dfrac{1}{4} = \dfrac{3}{4}$
- $P(X=2) = P(X=2,Y=1) + P(X=2,Y=2) = \dfrac{1}{4} + 0 = \dfrac{1}{4}$
Y的边缘分布律:
- $P(Y=1) = P(X=1,Y=1) + P(X=2,Y=1) = \dfrac{1}{2} + \dfrac{1}{4} = \dfrac{3}{4}$
- $P(Y=2) = P(X=1,Y=2) + P(X=2,Y=2) = \dfrac{1}{4} + 0 = \dfrac{1}{4}$
(2)求$D(X)$
- 计算$E(X)$:
$E(X) = 1 \cdot \dfrac{3}{4} + 2 \cdot \dfrac{1}{4} = \dfrac{5}{4}$ - 计算$E(X^2)$:
$E(X^2) = 1^2 \cdot \dfrac{3}{4} + 2^2 \cdot \dfrac{1}{4} = \dfrac{7}{4}$ - 代入方差公式:
$D(X) = E(X^2) - [E(X)]^2 = \dfrac{7}{4} - \left(\dfrac{5}{4}\right)^2 = \dfrac{3}{16}$
(3)求相关系数$\rho_{XY}$
- 计算$E(XY)$:
$E(XY) = 1 \cdot 1 \cdot \dfrac{1}{2} + 1 \cdot 2 \cdot \dfrac{1}{4} + 2 \cdot 1 \cdot \dfrac{1}{4} + 2 \cdot 2 \cdot 0 = \dfrac{3}{2}$ - 计算$E(Y)$和$E(Y^2)$:
$E(Y) = 1 \cdot \dfrac{3}{4} + 2 \cdot \dfrac{1}{4} = \dfrac{5}{4}$
$E(Y^2) = 1^2 \cdot \dfrac{3}{4} + 2^2 \cdot \dfrac{1}{4} = \dfrac{7}{4}$ - 计算协方差与标准差:
$\text{Cov}(X,Y) = E(XY) - E(X)E(Y) = \dfrac{3}{2} - \dfrac{5}{4} \cdot \dfrac{5}{4} = -\dfrac{1}{16}$
$\sigma_X = \sqrt{D(X)} = \sqrt{\dfrac{3}{16}} = \dfrac{\sqrt{3}}{4}, \quad \sigma_Y = \dfrac{\sqrt{3}}{4}$ - 计算相关系数:
$\rho_{XY} = \dfrac{\text{Cov}(X,Y)}{\sigma_X \sigma_Y} = \dfrac{-\dfrac{1}{16}}{\dfrac{3}{16}} = -\dfrac{1}{3}$