题目
5.2 找出下列各函数的所有零点.并指明其阶数:-|||-(1) dfrac ({z)^2+9}({z)^4};-|||-(2)zsinz;-|||-(3) ^2((e)^i-1).

题目解答
答案
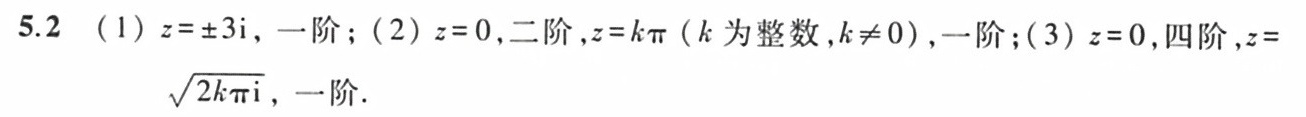
解析
步骤 1:分析函数 $\dfrac{{z}^{2}+9}{{z}^{4}}$
函数 $\dfrac{{z}^{2}+9}{{z}^{4}}$ 的零点是分子 ${z}^{2}+9$ 的零点,即 ${z}^{2}+9=0$ 的解。解这个方程,我们得到 $z=\pm 3i$。由于分母 ${z}^{4}$ 在 $z=0$ 处有四阶零点,而分子在 $z=0$ 处没有零点,所以 $z=0$ 不是函数的零点。$z=\pm 3i$ 是一阶零点,因为它们是 ${z}^{2}+9$ 的简单根。
步骤 2:分析函数 $z\sin z$
函数 $z\sin z$ 的零点是 $z=0$ 和 $\sin z=0$ 的解。$z=0$ 是二阶零点,因为 $z\sin z$ 在 $z=0$ 处的导数为 $0$。$\sin z=0$ 的解是 $z=k\pi$,其中 $k$ 是整数。这些点是一阶零点,因为 $\sin z$ 在这些点处的导数不为 $0$。
步骤 3:分析函数 ${z}^{2}({e}^{{z}^{2}}-1)$
函数 ${z}^{2}({e}^{{z}^{2}}-1)$ 的零点是 $z=0$ 和 ${e}^{{z}^{2}}-1=0$ 的解。$z=0$ 是四阶零点,因为 ${z}^{2}$ 在 $z=0$ 处有二阶零点,而 ${e}^{{z}^{2}}-1$ 在 $z=0$ 处也有二阶零点。${e}^{{z}^{2}}-1=0$ 的解是 ${z}^{2}=2k\pi i$,其中 $k$ 是整数。这些点是一阶零点,因为 ${e}^{{z}^{2}}-1$ 在这些点处的导数不为 $0$。
函数 $\dfrac{{z}^{2}+9}{{z}^{4}}$ 的零点是分子 ${z}^{2}+9$ 的零点,即 ${z}^{2}+9=0$ 的解。解这个方程,我们得到 $z=\pm 3i$。由于分母 ${z}^{4}$ 在 $z=0$ 处有四阶零点,而分子在 $z=0$ 处没有零点,所以 $z=0$ 不是函数的零点。$z=\pm 3i$ 是一阶零点,因为它们是 ${z}^{2}+9$ 的简单根。
步骤 2:分析函数 $z\sin z$
函数 $z\sin z$ 的零点是 $z=0$ 和 $\sin z=0$ 的解。$z=0$ 是二阶零点,因为 $z\sin z$ 在 $z=0$ 处的导数为 $0$。$\sin z=0$ 的解是 $z=k\pi$,其中 $k$ 是整数。这些点是一阶零点,因为 $\sin z$ 在这些点处的导数不为 $0$。
步骤 3:分析函数 ${z}^{2}({e}^{{z}^{2}}-1)$
函数 ${z}^{2}({e}^{{z}^{2}}-1)$ 的零点是 $z=0$ 和 ${e}^{{z}^{2}}-1=0$ 的解。$z=0$ 是四阶零点,因为 ${z}^{2}$ 在 $z=0$ 处有二阶零点,而 ${e}^{{z}^{2}}-1$ 在 $z=0$ 处也有二阶零点。${e}^{{z}^{2}}-1=0$ 的解是 ${z}^{2}=2k\pi i$,其中 $k$ 是整数。这些点是一阶零点,因为 ${e}^{{z}^{2}}-1$ 在这些点处的导数不为 $0$。