6.函数 =ln ((x)^2+(y)^2+(z)^2) 在点 M(1,2,-2) 处的梯度 (|)_(M)= __
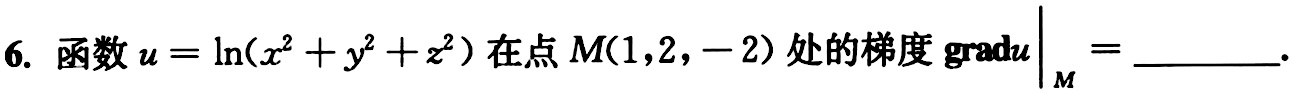
题目解答
答案
解析
考查要点:本题主要考查梯度的计算,需要掌握梯度的定义及对多元函数求偏导的方法。
解题核心思路:
- 梯度的定义:梯度是一个向量,其分量为函数对各个变量的偏导数,即 $\nabla u = \left( \dfrac{\partial u}{\partial x}, \dfrac{\partial u}{\partial y}, \dfrac{\partial u}{\partial z} \right)$。
- 链式法则求偏导:函数 $u = \ln(x^2 + y^2 + z^2)$ 的偏导数需通过链式法则计算,注意分母为公共项 $x^2 + y^2 + z^2$。
- 代入点坐标:将点 $M(1,2,-2)$ 代入偏导数表达式,计算具体数值。
破题关键点:
- 正确应用链式法则,避免漏乘变量系数。
- 分母统一计算:先计算公共分母 $x^2 + y^2 + z^2$ 的值,简化后续计算。
步骤1:计算偏导数
函数 $u = \ln(x^2 + y^2 + z^2)$,对 $x$ 求偏导:
$\dfrac{\partial u}{\partial x} = \dfrac{1}{x^2 + y^2 + z^2} \cdot 2x = \dfrac{2x}{x^2 + y^2 + z^2}$
同理,对 $y$ 和 $z$ 求偏导:
$\dfrac{\partial u}{\partial y} = \dfrac{2y}{x^2 + y^2 + z^2}, \quad \dfrac{\partial u}{\partial z} = \dfrac{2z}{x^2 + y^2 + z^2}$
步骤2:代入点 $M(1,2,-2)$
-
计算分母:
$x^2 + y^2 + z^2 = 1^2 + 2^2 + (-2)^2 = 1 + 4 + 4 = 9$ -
计算各偏导数值:
$\dfrac{\partial u}{\partial x}\bigg|_M = \dfrac{2 \cdot 1}{9} = \dfrac{2}{9}, \quad \dfrac{\partial u}{\partial y}\bigg|_M = \dfrac{2 \cdot 2}{9} = \dfrac{4}{9}, \quad \dfrac{\partial u}{\partial z}\bigg|_M = \dfrac{2 \cdot (-2)}{9} = -\dfrac{4}{9}$
步骤3:写出梯度向量
$\nabla u\bigg|_M = \left( \dfrac{2}{9}, \dfrac{4}{9}, -\dfrac{4}{9} \right)$