题目
5. 级数 sum _(n=1)^infty dfrac ({(-1))^n}({n)^p} 当 () .-|||-(A) gt 1 时条件收敛; (B) lt pleqslant 1 时条件收敛;-|||-(C) lt pleqslant 1 时绝对收敛; (D) lt pleqslant 1 时发散.
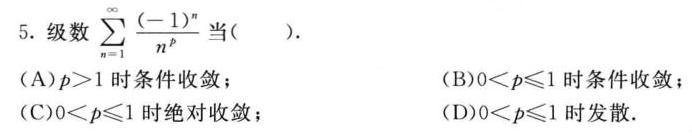
题目解答
答案

解析
步骤 1:判断级数的类型
级数 $\sum _{n=1}^{\infty }\dfrac {{(-1)}^{n}}{{n}^{p}}$ 是一个交错级数,因为每一项的符号交替变化。
步骤 2:应用莱布尼兹审敛法
根据莱布尼兹审敛法,如果一个交错级数 $\sum _{n=1}^{\infty }(-1)^{n}a_{n}$ 满足以下条件,则该级数收敛:
1. $a_{n} \geq 0$ 对所有 $n$ 成立;
2. $a_{n}$ 是单调递减的;
3. $\lim _{n\to \infty }a_{n}=0$。
对于级数 $\sum _{n=1}^{\infty }\dfrac {{(-1)}^{n}}{{n}^{p}}$,我们有 $a_{n}=\dfrac {1}{{n}^{p}}$。当 $p>0$ 时,$a_{n}$ 满足上述条件,因此级数收敛。
步骤 3:判断绝对收敛性
为了判断级数的绝对收敛性,我们需要考虑级数 $\sum _{n=1}^{\infty }|\dfrac {{(-1)}^{n}}{{n}^{p}}|=\sum _{n=1}^{\infty }\dfrac {1}{{n}^{p}}$ 的收敛性。根据 $p$-级数的收敛性,当 $p>1$ 时,级数 $\sum _{n=1}^{\infty }\dfrac {1}{{n}^{p}}$ 收敛;当 $0
级数 $\sum _{n=1}^{\infty }\dfrac {{(-1)}^{n}}{{n}^{p}}$ 是一个交错级数,因为每一项的符号交替变化。
步骤 2:应用莱布尼兹审敛法
根据莱布尼兹审敛法,如果一个交错级数 $\sum _{n=1}^{\infty }(-1)^{n}a_{n}$ 满足以下条件,则该级数收敛:
1. $a_{n} \geq 0$ 对所有 $n$ 成立;
2. $a_{n}$ 是单调递减的;
3. $\lim _{n\to \infty }a_{n}=0$。
对于级数 $\sum _{n=1}^{\infty }\dfrac {{(-1)}^{n}}{{n}^{p}}$,我们有 $a_{n}=\dfrac {1}{{n}^{p}}$。当 $p>0$ 时,$a_{n}$ 满足上述条件,因此级数收敛。
步骤 3:判断绝对收敛性
为了判断级数的绝对收敛性,我们需要考虑级数 $\sum _{n=1}^{\infty }|\dfrac {{(-1)}^{n}}{{n}^{p}}|=\sum _{n=1}^{\infty }\dfrac {1}{{n}^{p}}$ 的收敛性。根据 $p$-级数的收敛性,当 $p>1$ 时,级数 $\sum _{n=1}^{\infty }\dfrac {1}{{n}^{p}}$ 收敛;当 $0