3.设A,B为两事件,已知 (A)=dfrac (1)(3) . (A|B)=dfrac (2)(3) . (B|overline (A))=dfrac (1)(10), 求P(B).
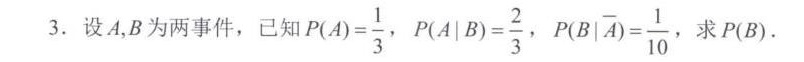
题目解答
答案
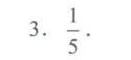
解析
考查要点:本题主要考查条件概率的定义及全概率公式的应用,需要学生理解事件间的关系并建立方程求解。
解题核心思路:
- 分解事件:将事件$B$分解为与$A$相关的部分$B \cap A$和与$\overline{A}$相关的部分$B \cap \overline{A}$。
- 利用条件概率公式:通过已知的条件概率$P(A|B)$和$P(B|\overline{A})$,分别表示出$P(B \cap A)$和$P(B \cap \overline{A})$。
- 全概率公式:将$P(B)$表示为两部分概率之和,建立方程求解。
破题关键点:
- 正确应用条件概率公式,将未知量用$P(B)$表示。
- 建立方程时注意代数运算的准确性。
步骤1:分解事件$B$
根据全概率公式,事件$B$可分解为:
$P(B) = P(B \cap A) + P(B \cap \overline{A})$
步骤2:计算$P(B \cap A)$
由条件概率公式$P(A|B) = \dfrac{P(B \cap A)}{P(B)}$,得:
$P(B \cap A) = P(A|B) \cdot P(B) = \dfrac{2}{3} P(B)$
步骤3:计算$P(B \cap \overline{A})$
由条件概率公式$P(B|\overline{A}) = \dfrac{P(B \cap \overline{A})}{P(\overline{A})}$,得:
$P(B \cap \overline{A}) = P(B|\overline{A}) \cdot P(\overline{A}) = \dfrac{1}{10} \cdot \left(1 - \dfrac{1}{3}\right) = \dfrac{1}{10} \cdot \dfrac{2}{3} = \dfrac{1}{15}$
步骤4:建立方程求解$P(B)$
将步骤2和步骤3的结果代入全概率公式:
$P(B) = \dfrac{2}{3} P(B) + \dfrac{1}{15}$
整理方程:
$P(B) - \dfrac{2}{3} P(B) = \dfrac{1}{15} \implies \dfrac{1}{3} P(B) = \dfrac{1}{15} \implies P(B) = \dfrac{1}{5}$