题目
设曲线口为口在第一象限部分，则曲线积分口( )A. 口B. 口C. 口D. 口
设曲线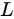
为
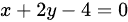在第一象限部分，则曲线积分
( )
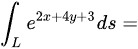A.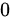 
B.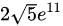 
C.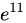 
D.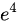 
题目解答
答案
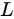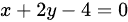解：已知曲线为在第一象限部分，
则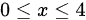
，
由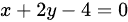得：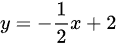
，
求导得：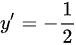
，
于是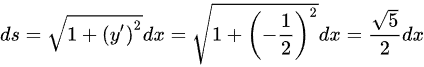
，所以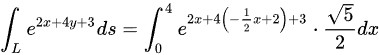
.
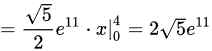故答案为：B.
解析
步骤 1：确定曲线的范围
曲线方程为x+2y-4=0，且在第一象限部分，因此x和y都大于0。解方程得到y关于x的表达式，即$y=-\dfrac {1}{2}x+2$。由于x和y都大于0，可以得到x的范围为$0\leqslant x\leqslant 4$。
步骤 2：计算ds
曲线积分中，ds表示曲线上的微小弧长。对于给定的曲线，ds可以表示为$ds=\sqrt {1+{(y')}^{2}}dx$。其中，$y'$是y关于x的导数。对于给定的曲线，$y'=-\dfrac {1}{2}$，因此$ds=\sqrt {1+{(-\dfrac {1}{2})}^{2}}dx=\dfrac {\sqrt {5}}{2}dx$。
步骤 3：计算曲线积分
将ds代入曲线积分中，得到${\int }_{L}^{2x+4y+3}ds={\int }_{0}^{4}{e}^{2x+4(-\dfrac {1}{2}x+2)+3}\cdot \dfrac {\sqrt {5}}{2}dx$。化简后得到${\int }_{0}^{4}{e}^{2x+4}(-\dfrac {1}{2}x+2)+3\cdot \dfrac {\sqrt {5}}{2}dx$。进一步化简得到${\int }_{0}^{4}{e}^{11}\cdot \dfrac {\sqrt {5}}{2}dx$。计算积分得到$\dfrac {\sqrt {5}}{2}{e}^{11}\cdot x{|}_{0}^{4}=2\sqrt {5}{e}^{11}$。
曲线方程为x+2y-4=0，且在第一象限部分，因此x和y都大于0。解方程得到y关于x的表达式，即$y=-\dfrac {1}{2}x+2$。由于x和y都大于0，可以得到x的范围为$0\leqslant x\leqslant 4$。
步骤 2：计算ds
曲线积分中，ds表示曲线上的微小弧长。对于给定的曲线，ds可以表示为$ds=\sqrt {1+{(y')}^{2}}dx$。其中，$y'$是y关于x的导数。对于给定的曲线，$y'=-\dfrac {1}{2}$，因此$ds=\sqrt {1+{(-\dfrac {1}{2})}^{2}}dx=\dfrac {\sqrt {5}}{2}dx$。
步骤 3：计算曲线积分
将ds代入曲线积分中，得到${\int }_{L}^{2x+4y+3}ds={\int }_{0}^{4}{e}^{2x+4(-\dfrac {1}{2}x+2)+3}\cdot \dfrac {\sqrt {5}}{2}dx$。化简后得到${\int }_{0}^{4}{e}^{2x+4}(-\dfrac {1}{2}x+2)+3\cdot \dfrac {\sqrt {5}}{2}dx$。进一步化简得到${\int }_{0}^{4}{e}^{11}\cdot \dfrac {\sqrt {5}}{2}dx$。计算积分得到$\dfrac {\sqrt {5}}{2}{e}^{11}\cdot x{|}_{0}^{4}=2\sqrt {5}{e}^{11}$。