题目
4.设矩阵A= a 1 3 0 1 b 0 0 2 与矩阵B= 1 0 0 1 1 1 1 -1 3 相似,则 ()-|||-y-|||-(A) =2, =-3; (B) =2, neq -3; (C) neq 2, =-3; (D) neq 2b=
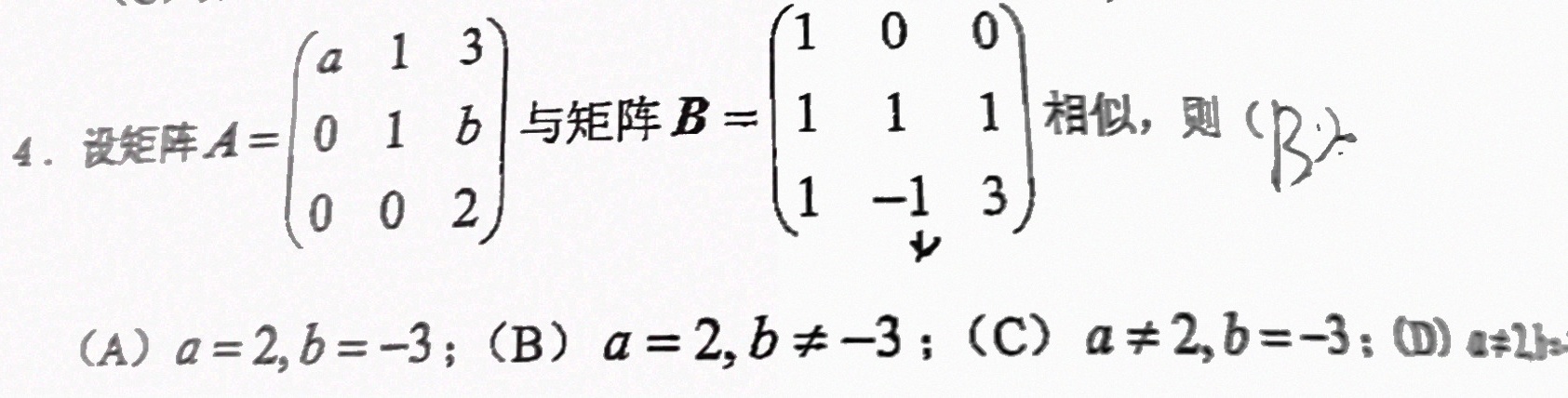
题目解答
答案

解析
矩阵相似的条件是解题的核心。相似矩阵必须满足以下条件:
- 特征值相同(包括代数重数);
- 几何重数相同(对应Jordan块结构一致);
- 秩、迹、行列式相等。
本题中,矩阵$A$和$B$相似,需通过特征值、几何重数等条件确定$a$和$b$的值。
步骤1:计算特征值
-
矩阵$B$的特征多项式为:
$\det(B-\lambda I) = (1-\lambda)(\lambda-2)^2$
特征值为$\lambda=1$(代数重数1)和$\lambda=2$(代数重数2)。 -
矩阵$A$为上三角矩阵,特征值为$a,1,2$。为与$B$的特征值一致,需$a=2$。
步骤2:验证几何重数
- 矩阵$B$中,$\lambda=2$的几何重数为1(通过秩计算)。
- 矩阵$A$中,当$a=2$时,$A-2I$的秩为:
- 若$b \neq -3$,秩为2,几何重数为1,与$B$一致;
- 若$b = -3$,秩为1,几何重数为2,与$B$不一致。
因此,必须满足$b \neq -3$。