14.设二维随机变量(X,Y)的联合概率密度为-|||-f(x,y)= ) 3x,0lt xlt 1,0lt ylt x 0, .-|||-问X与Y是否相互独立?

考查要点：本题主要考查二维随机变量的独立性判断，需要掌握边缘概率密度的计算方法以及独立性的判定条件。

解题核心思路：

1. 计算边缘概率密度：分别对X和Y求边缘密度$f_X(x)$和$f_Y(y)$。
2. 验证乘积关系：检查是否存在$f(x,y) = f_X(x) \cdot f_Y(y)$，若存在任意一点不满足，则X与Y不独立。

破题关键点：

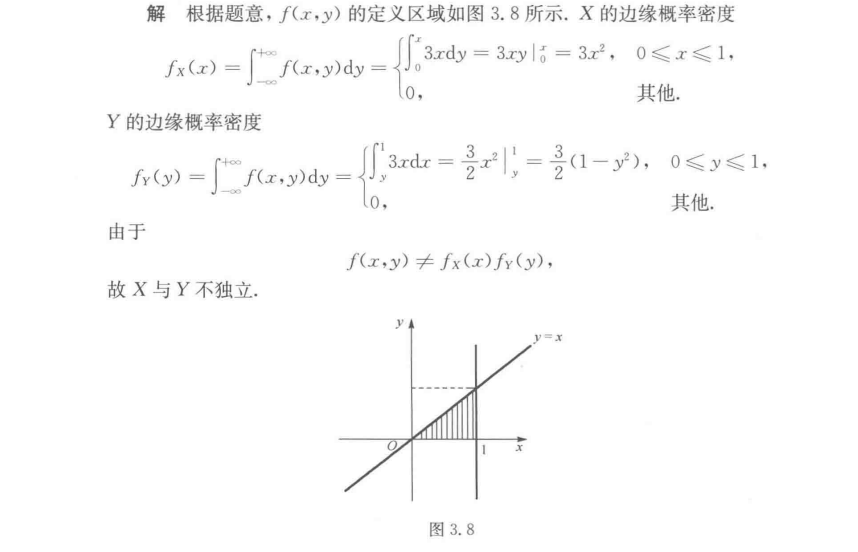
• 积分区域的确定：联合密度$f(x,y)$的非零区域为$0 < y < x < 1$，需注意积分上下限。
• 独立性判定：通过比较$f(x,y)$与$f_X(x)f_Y(y)$是否相等得出结论。

计算X的边缘概率密度$f_X(x)$

对$y$积分，积分区间为$0 < y < x$：
$f_X(x) = \int_{-\infty}^{+\infty} f(x,y) \, dy = \int_{0}^{x} 3x \, dy = 3x \cdot \left[ y \right]_0^x = 3x^2 \quad (0 \leq x \leq 1)$

计算Y的边缘概率密度$f_Y(y)$

对$x$积分，积分区间为$y < x < 1$：
$f_Y(y) = \int_{-\infty}^{+\infty} f(x,y) \, dx = \int_{y}^{1} 3x \, dx = \frac{3}{2} \left[ x^2 \right]_y^1 = \frac{3}{2}(1 - y^2) \quad (0 \leq y \leq 1)$

验证独立性

若X与Y独立，则$f(x,y) = f_X(x) \cdot f_Y(y)$。计算乘积：
$f_X(x) \cdot f_Y(y) = 3x^2 \cdot \frac{3}{2}(1 - y^2) = \frac{9}{2}x^2(1 - y^2)$
而原联合密度为$f(x,y) = 3x$，显然：
$3x \neq \frac{9}{2}x^2(1 - y^2)$
因此，$f(x,y) \neq f_X(x) \cdot f_Y(y)$，X与Y不独立。