题目
求过点(-1,0,4),且平行于平面3x-4y+z-10=0,又与直线3x-4y+z-10=0相交的直线的方程.
求过点$(-1,0,4)$,且平行于平面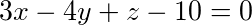 ,又与直线
,又与直线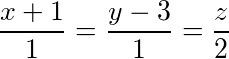 相交的直线的方程.
相交的直线的方程.
题目解答
答案
设所求直线方程为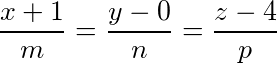 .
.
所求直线平行于平面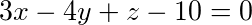 ,故有
,故有
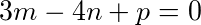 , (1)
, (1)
又所求直线与直线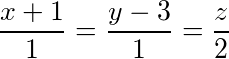 相交,故有
相交,故有
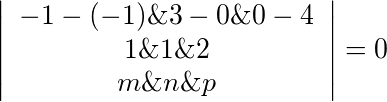 ,
,
即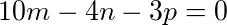 . (2)
. (2)
联立(1)(2)式可得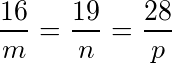 .
.
因此所求直线方程为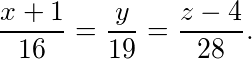
解析
步骤 1:确定所求直线的方向向量
设所求直线方程为$\dfrac {x+1}{m}=\dfrac {y-0}{n}=\dfrac {z-4}{p}$,其中$m,n,p$为所求直线的方向向量的分量。
步骤 2:利用直线与平面平行的条件
所求直线平行于平面3x-4y+z-10=0,故有
3m-4n+p=0, (1)
步骤 3:利用直线与已知直线相交的条件
所求直线与直线$\dfrac {x+1}{1}=\dfrac {y-3}{1}=\dfrac {z}{2}$相交,故有
$-1-(-1)\& 3-0\& 0-4$ $18182$ $mgndpp$,
即10m-4n-3p=0. (2)
步骤 4:联立方程求解
联立(1)(2)式可得$\dfrac {16}{m}=\dfrac {19}{n}=\dfrac {28}{p}$.
设所求直线方程为$\dfrac {x+1}{m}=\dfrac {y-0}{n}=\dfrac {z-4}{p}$,其中$m,n,p$为所求直线的方向向量的分量。
步骤 2:利用直线与平面平行的条件
所求直线平行于平面3x-4y+z-10=0,故有
3m-4n+p=0, (1)
步骤 3:利用直线与已知直线相交的条件
所求直线与直线$\dfrac {x+1}{1}=\dfrac {y-3}{1}=\dfrac {z}{2}$相交,故有
$-1-(-1)\& 3-0\& 0-4$ $18182$ $mgndpp$,
即10m-4n-3p=0. (2)
步骤 4:联立方程求解
联立(1)(2)式可得$\dfrac {16}{m}=\dfrac {19}{n}=\dfrac {28}{p}$.