题目
设 L 是抛物线=dfrac (1)(4)(x)^2上 点=dfrac (1)(4)(x)^2与 点=dfrac (1)(4)(x)^2 的一段弧则=dfrac (1)(4)(x)^2 ()A. =dfrac (1)(4)(x)^2 B. =dfrac (1)(4)(x)^2C. =dfrac (1)(4)(x)^2D. =dfrac (1)(4)(x)^2
设 L 是抛物线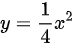 上 点
上 点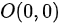 与 点
与 点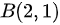 的一段弧则
的一段弧则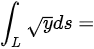 ()
()
A. 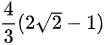
B. 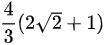
C. 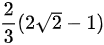
D. 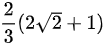
题目解答
答案
设 L 是抛物线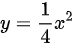 上点 O(0,0) 与点 B(2,1) 的一段弧。
上点 O(0,0) 与点 B(2,1) 的一段弧。
则 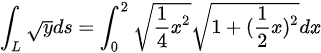
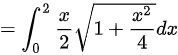 。
。
令 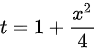 ,则
,则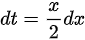 ,所以
,所以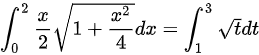 。
。
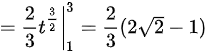 。
。
因此,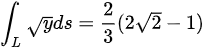 . 答案选C。
. 答案选C。
解析
步骤 1:确定积分的参数化
抛物线$y=\dfrac {1}{4}{x}^{2}$上从点(0,0)到点(2,1)的一段弧可以参数化为$x=t$,$y=\dfrac {1}{4}{t}^{2}$,其中$t$从0变到2。
步骤 2:计算弧长微分$ds$
根据参数化,$ds=\sqrt {1+{(\dfrac {dy}{dx})}^{2}}dx=\sqrt {1+{(\dfrac {1}{2}t)}^{2}}dt=\sqrt {1+\dfrac {{t}^{2}}{4}}dt$。
步骤 3:计算积分
${\int }_{L}\sqrt {y}ds={\int }_{0}^{2}\sqrt {\dfrac {1}{4}{t}^{2}}\sqrt {1+\dfrac {{t}^{2}}{4}}dt={\int }_{0}^{2}\dfrac {t}{2}\sqrt {1+\dfrac {{t}^{2}}{4}}dt$。
步骤 4:换元积分
令$t=2\sinh(u)$,则$dt=2\cosh(u)du$,且当$t=0$时,$u=0$;当$t=2$时,$u=\sinh^{-1}(1)$。因此,积分变为${\int }_{0}^{\sinh^{-1}(1)}\sinh(u)\sqrt {1+\sinh^{2}(u)}2\cosh(u)du={\int }_{0}^{\sinh^{-1}(1)}2\sinh(u)\cosh^{2}(u)du$。
步骤 5:计算积分结果
${\int }_{0}^{\sinh^{-1}(1)}2\sinh(u)\cosh^{2}(u)du=\dfrac {2}{3}\cosh^{3}(u)|_{0}^{\sinh^{-1}(1)}=\dfrac {2}{3}(\cosh^{3}(\sinh^{-1}(1))-\cosh^{3}(0))=\dfrac {2}{3}(2\sqrt {2}-1)$。
抛物线$y=\dfrac {1}{4}{x}^{2}$上从点(0,0)到点(2,1)的一段弧可以参数化为$x=t$,$y=\dfrac {1}{4}{t}^{2}$,其中$t$从0变到2。
步骤 2:计算弧长微分$ds$
根据参数化,$ds=\sqrt {1+{(\dfrac {dy}{dx})}^{2}}dx=\sqrt {1+{(\dfrac {1}{2}t)}^{2}}dt=\sqrt {1+\dfrac {{t}^{2}}{4}}dt$。
步骤 3:计算积分
${\int }_{L}\sqrt {y}ds={\int }_{0}^{2}\sqrt {\dfrac {1}{4}{t}^{2}}\sqrt {1+\dfrac {{t}^{2}}{4}}dt={\int }_{0}^{2}\dfrac {t}{2}\sqrt {1+\dfrac {{t}^{2}}{4}}dt$。
步骤 4:换元积分
令$t=2\sinh(u)$,则$dt=2\cosh(u)du$,且当$t=0$时,$u=0$;当$t=2$时,$u=\sinh^{-1}(1)$。因此,积分变为${\int }_{0}^{\sinh^{-1}(1)}\sinh(u)\sqrt {1+\sinh^{2}(u)}2\cosh(u)du={\int }_{0}^{\sinh^{-1}(1)}2\sinh(u)\cosh^{2}(u)du$。
步骤 5:计算积分结果
${\int }_{0}^{\sinh^{-1}(1)}2\sinh(u)\cosh^{2}(u)du=\dfrac {2}{3}\cosh^{3}(u)|_{0}^{\sinh^{-1}(1)}=\dfrac {2}{3}(\cosh^{3}(\sinh^{-1}(1))-\cosh^{3}(0))=\dfrac {2}{3}(2\sqrt {2}-1)$。