题目
已知甲袋中装有3只红球,2只白球,乙袋中装有 6 只红球4只白球,丙袋中装有 2 只红球 ,8只白球,随机地取一只袋子 ,再从该袋中随机地取一只球,求该球是红球的概率。
已知甲袋中装有3只红球,2只白球,乙袋中装有 6 只红球4只白球,丙袋中装有 2 只红球 ,8只白球,随机地取一只袋子 ,再从该袋中随机地取一只球,求该球是红球的概率。
题目解答
答案
记事件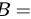 “取出的球为红球”,事件
“取出的球为红球”,事件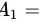 "该球来自甲袋",事件
"该球来自甲袋",事件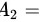 “该球来自乙袋”,事件
“该球来自乙袋”,事件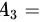 “该球来自丙袋”,则由题意得
“该球来自丙袋”,则由题意得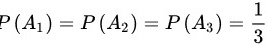
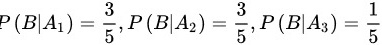
则根据全概率公式可知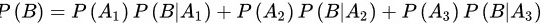
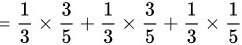
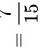
故答案为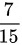 。
。
解析
考查要点:本题主要考查全概率公式的应用,涉及条件概率的计算和互斥事件的概率叠加。
解题核心思路:
- 确定互斥且穷尽的事件:选择甲、乙、丙三个袋子中的任意一个,这三个事件互斥且概率之和为1。
- 计算每个事件下的条件概率:分别求出从每个袋子中取出红球的概率。
- 应用全概率公式:将每个袋子被选中的概率与对应条件概率相乘后求和,得到最终结果。
破题关键点:
- 正确识别每个袋子的红球比例,避免计算错误。
- 确保全概率公式中的权重(袋子被选中的概率)分配正确,本题中每个袋子被选中的概率均为$\dfrac{1}{3}$。
步骤1:定义事件
- 事件$A_1$:选中甲袋;
- 事件$A_2$:选中乙袋;
- 事件$A_3$:选中丙袋;
- 事件$B$:取出的球是红球。
步骤2:计算各事件的概率
- 选袋概率:$P(A_1) = P(A_2) = P(A_3) = \dfrac{1}{3}$。
- 条件概率:
- 甲袋红球概率:$P(B|A_1) = \dfrac{3}{3+2} = \dfrac{3}{5}$;
- 乙袋红球概率:$P(B|A_2) = \dfrac{6}{6+4} = \dfrac{3}{5}$;
- 丙袋红球概率:$P(B|A_3) = \dfrac{2}{2+8} = \dfrac{1}{5}$。
步骤3:应用全概率公式
$\begin{aligned}P(B) &= P(A_1)P(B|A_1) + P(A_2)P(B|A_2) + P(A_3)P(B|A_3) \\&= \dfrac{1}{3} \times \dfrac{3}{5} + \dfrac{1}{3} \times \dfrac{3}{5} + \dfrac{1}{3} \times \dfrac{1}{5} \\&= \dfrac{3}{15} + \dfrac{3}{15} + \dfrac{1}{15} \\&= \dfrac{7}{15}.\end{aligned}$