题目
求方程 dfrac (dy)(dx)=dfrac (x+2y+1)(2x+4y-1) 的通解.
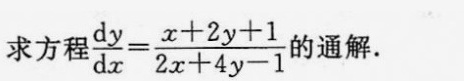
题目解答
答案

解析
步骤 1:判断方程类型
方程 $\dfrac {dy}{dx}=\dfrac {x+2y+1}{2x+4y-1}$ 是一个一阶非线性微分方程。由于分子和分母都是关于 $x$ 和 $y$ 的一次多项式,且系数矩阵的行列式为零,即 $|\begin{matrix} 1& 2\\ 2& 4\end{matrix} |=0$,因此可以尝试通过变量替换将其化为可分离变量的方程。
步骤 2:变量替换
令 $z=x+2y$,则 $\dfrac {dz}{dx}=1+2\dfrac {dy}{dx}$。将原方程中的 $y$ 用 $z$ 表示,即 $y=\dfrac{z-x}{2}$,代入原方程,得到 $\dfrac {dz}{dx}=1+\dfrac {2(z+1)}{2z-1}$,即 $\dfrac {dz}{dx}=\dfrac {4z+1}{2z-1}$。
步骤 3:分离变量并求解
将方程 $\dfrac {dz}{dx}=\dfrac {4z+1}{2z-1}$ 分离变量,得到 $\dfrac{2z-1}{4z+1}dz=dx$。对两边积分,得到 $\int \dfrac{2z-1}{4z+1}dz=\int dx$。通过部分分式分解,可以将左边的积分化简为 $\int \left(\dfrac{1}{2}-\dfrac{3}{2(4z+1)}\right)dz$,从而得到 $\dfrac{z}{2}-\dfrac{3}{8}\ln|4z+1|=x+C$。将 $z=x+2y$ 代入,得到 $\dfrac{x+2y}{2}-\dfrac{3}{8}\ln|4x+8y+1|=x+C$,化简得到 $8y-4x-3\ln|4x+8y+1|=C$。
步骤 4:考虑特殊情况
除了上述通解外,还需要考虑 $4x+8y+1=0$ 的情况,因为当 $4x+8y+1=0$ 时,原方程的分母为零,因此 $4x+8y+1=0$ 也是原方程的解。
方程 $\dfrac {dy}{dx}=\dfrac {x+2y+1}{2x+4y-1}$ 是一个一阶非线性微分方程。由于分子和分母都是关于 $x$ 和 $y$ 的一次多项式,且系数矩阵的行列式为零,即 $|\begin{matrix} 1& 2\\ 2& 4\end{matrix} |=0$,因此可以尝试通过变量替换将其化为可分离变量的方程。
步骤 2:变量替换
令 $z=x+2y$,则 $\dfrac {dz}{dx}=1+2\dfrac {dy}{dx}$。将原方程中的 $y$ 用 $z$ 表示,即 $y=\dfrac{z-x}{2}$,代入原方程,得到 $\dfrac {dz}{dx}=1+\dfrac {2(z+1)}{2z-1}$,即 $\dfrac {dz}{dx}=\dfrac {4z+1}{2z-1}$。
步骤 3:分离变量并求解
将方程 $\dfrac {dz}{dx}=\dfrac {4z+1}{2z-1}$ 分离变量,得到 $\dfrac{2z-1}{4z+1}dz=dx$。对两边积分,得到 $\int \dfrac{2z-1}{4z+1}dz=\int dx$。通过部分分式分解,可以将左边的积分化简为 $\int \left(\dfrac{1}{2}-\dfrac{3}{2(4z+1)}\right)dz$,从而得到 $\dfrac{z}{2}-\dfrac{3}{8}\ln|4z+1|=x+C$。将 $z=x+2y$ 代入,得到 $\dfrac{x+2y}{2}-\dfrac{3}{8}\ln|4x+8y+1|=x+C$,化简得到 $8y-4x-3\ln|4x+8y+1|=C$。
步骤 4:考虑特殊情况
除了上述通解外,还需要考虑 $4x+8y+1=0$ 的情况,因为当 $4x+8y+1=0$ 时,原方程的分母为零,因此 $4x+8y+1=0$ 也是原方程的解。