题目
(15)(本题满分10分)-|||-求曲线 =dfrac ({x)^1+x}({(1+x))^x}(xgt 0) 的斜渐近线方程.
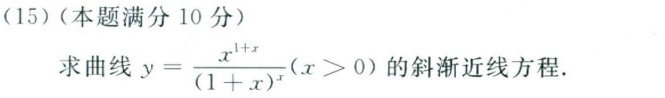
题目解答
答案
解:


解析
步骤 1:计算斜率 a
为了找到斜渐近线的斜率 a,我们需要计算 $\lim _{x\rightarrow +\infty }\dfrac {y}{x}$。将给定的函数代入,我们得到:
$$
\lim _{x\rightarrow +\infty }\dfrac {y}{x}=\lim _{x\rightarrow +\infty }\dfrac {{x}^{1+x}}{x{(1+x)}^{x}}=\lim _{x\rightarrow +\infty }\dfrac {{x}^{x}}{{(1+x)}^{x}}=\lim _{x\rightarrow +\infty }\dfrac {1}{{(1+\dfrac {1}{x})}^{x}}=\dfrac {1}{e}=a
$$
步骤 2:计算截距 b
为了找到斜渐近线的截距 b,我们需要计算 $\lim _{x\rightarrow +\infty }[ y-\omega x]$。将给定的函数代入,我们得到:
$$
\lim _{x\rightarrow +\infty }[ y-\omega x] =\lim _{x\rightarrow +\infty }[ \dfrac {{x}^{1+x}}{{(1+x)}^{x}}-\dfrac {x}{e}] =\lim _{x\rightarrow +\infty }\dfrac {x[ e-{(1+\dfrac {1}{x})}^{x}] }{x(1+\dfrac {1}{x})}
$$
令 $t=\dfrac {1}{x}$,则 $t\rightarrow 0^{+}$ 时,我们有:
$$
\lim _{t\rightarrow {0}^{+}}\dfrac {{(1+t)}^{\dfrac {1}{t}}-e}{t}=\dfrac {-1}{{e}^{2}}\lim _{t\rightarrow {0}^{+}}\dfrac {{e}^{-\dfrac {e(1+t)}{t}}-1}{t}=-\dfrac {1}{e}\lim _{t\rightarrow {0}^{+}}\dfrac {\ln (1+t)-t}{{t}^{2}}=-\dfrac {1}{e}\lim _{t\rightarrow {0}^{+}}\dfrac {-\dfrac {1}{2}{t}^{2}}{{t}^{2}}=\dfrac {1}{2e}=b
$$
步骤 3:写出斜渐近线方程
根据斜率 a 和截距 b,斜渐近线方程为:
$$
y=ax+b=\dfrac {1}{e}x+\dfrac {1}{2e}
$$
为了找到斜渐近线的斜率 a,我们需要计算 $\lim _{x\rightarrow +\infty }\dfrac {y}{x}$。将给定的函数代入,我们得到:
$$
\lim _{x\rightarrow +\infty }\dfrac {y}{x}=\lim _{x\rightarrow +\infty }\dfrac {{x}^{1+x}}{x{(1+x)}^{x}}=\lim _{x\rightarrow +\infty }\dfrac {{x}^{x}}{{(1+x)}^{x}}=\lim _{x\rightarrow +\infty }\dfrac {1}{{(1+\dfrac {1}{x})}^{x}}=\dfrac {1}{e}=a
$$
步骤 2:计算截距 b
为了找到斜渐近线的截距 b,我们需要计算 $\lim _{x\rightarrow +\infty }[ y-\omega x]$。将给定的函数代入,我们得到:
$$
\lim _{x\rightarrow +\infty }[ y-\omega x] =\lim _{x\rightarrow +\infty }[ \dfrac {{x}^{1+x}}{{(1+x)}^{x}}-\dfrac {x}{e}] =\lim _{x\rightarrow +\infty }\dfrac {x[ e-{(1+\dfrac {1}{x})}^{x}] }{x(1+\dfrac {1}{x})}
$$
令 $t=\dfrac {1}{x}$,则 $t\rightarrow 0^{+}$ 时,我们有:
$$
\lim _{t\rightarrow {0}^{+}}\dfrac {{(1+t)}^{\dfrac {1}{t}}-e}{t}=\dfrac {-1}{{e}^{2}}\lim _{t\rightarrow {0}^{+}}\dfrac {{e}^{-\dfrac {e(1+t)}{t}}-1}{t}=-\dfrac {1}{e}\lim _{t\rightarrow {0}^{+}}\dfrac {\ln (1+t)-t}{{t}^{2}}=-\dfrac {1}{e}\lim _{t\rightarrow {0}^{+}}\dfrac {-\dfrac {1}{2}{t}^{2}}{{t}^{2}}=\dfrac {1}{2e}=b
$$
步骤 3:写出斜渐近线方程
根据斜率 a 和截距 b,斜渐近线方程为:
$$
y=ax+b=\dfrac {1}{e}x+\dfrac {1}{2e}
$$