题目
证明:级数sum _(n=1)^infty (sin dfrac (1)({n)^2})收敛。
证明:级数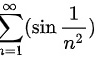 收敛。
收敛。
题目解答
答案
证明:
要证明级数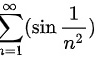 收敛,我们可以使用比较判别法,我们将该级数与一个已知收敛的级数进行比较。
收敛,我们可以使用比较判别法,我们将该级数与一个已知收敛的级数进行比较。
首先,注意到对于任意正整数n,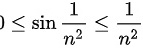 ,
,
这是因为正弦函数的值范围在 -1到1之间,而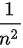 是一个递减的正项数列。现在,我们考虑级数
是一个递减的正项数列。现在,我们考虑级数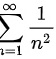 ,这是一个已知的收敛的 p级数,因为p级数
,这是一个已知的收敛的 p级数,因为p级数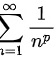 在
在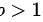 1" data-width="48" data-height="22" data-size="686" data-format="png" style="max-width:100%">时收敛,在这里p=2,所以级数
1" data-width="48" data-height="22" data-size="686" data-format="png" style="max-width:100%">时收敛,在这里p=2,所以级数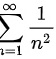 收敛。
收敛。
由于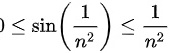 ,对于所有正整数n成立,并且级数
,对于所有正整数n成立,并且级数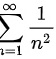 收敛,根据比较判别法,我们可以得出结论:级数
收敛,根据比较判别法,我们可以得出结论:级数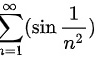 收敛,即证。
收敛,即证。
解析
步骤 1:比较判别法
比较判别法是判断级数收敛性的一种方法,它通过将待判断的级数与一个已知收敛或发散的级数进行比较来得出结论。如果待判断级数的每一项都小于或等于一个已知收敛级数的对应项,那么待判断级数也收敛。
步骤 2:确定比较级数
我们选择级数$\sum _{n=1}^{\infty }\dfrac {1}{{n}^{2}}$作为比较级数。这是一个p级数,其中$p=2$。根据p级数的收敛性,当$p>1$时,级数收敛。因此,$\sum _{n=1}^{\infty }\dfrac {1}{{n}^{2}}$收敛。
步骤 3:比较级数项
对于任意正整数$n$,我们有$0\leqslant \sin \dfrac {1}{{n}^{2}}\leqslant \dfrac {1}{{n}^{2}}$。这是因为正弦函数的值域在$[-1,1]$之间,而$\dfrac {1}{{n}^{2}}$是一个递减的正项数列。因此,级数$\sum _{n=1}^{\infty }(\sin \dfrac {1}{{n}^{2}})$的每一项都小于或等于级数$\sum _{n=1}^{\infty }\dfrac {1}{{n}^{2}}$的对应项。
步骤 4:应用比较判别法
由于级数$\sum _{n=1}^{\infty }\dfrac {1}{{n}^{2}}$收敛,且级数$\sum _{n=1}^{\infty }(\sin \dfrac {1}{{n}^{2}})$的每一项都小于或等于级数$\sum _{n=1}^{\infty }\dfrac {1}{{n}^{2}}$的对应项,根据比较判别法,级数$\sum _{n=1}^{\infty }(\sin \dfrac {1}{{n}^{2}})$也收敛。
比较判别法是判断级数收敛性的一种方法,它通过将待判断的级数与一个已知收敛或发散的级数进行比较来得出结论。如果待判断级数的每一项都小于或等于一个已知收敛级数的对应项,那么待判断级数也收敛。
步骤 2:确定比较级数
我们选择级数$\sum _{n=1}^{\infty }\dfrac {1}{{n}^{2}}$作为比较级数。这是一个p级数,其中$p=2$。根据p级数的收敛性,当$p>1$时,级数收敛。因此,$\sum _{n=1}^{\infty }\dfrac {1}{{n}^{2}}$收敛。
步骤 3:比较级数项
对于任意正整数$n$,我们有$0\leqslant \sin \dfrac {1}{{n}^{2}}\leqslant \dfrac {1}{{n}^{2}}$。这是因为正弦函数的值域在$[-1,1]$之间,而$\dfrac {1}{{n}^{2}}$是一个递减的正项数列。因此,级数$\sum _{n=1}^{\infty }(\sin \dfrac {1}{{n}^{2}})$的每一项都小于或等于级数$\sum _{n=1}^{\infty }\dfrac {1}{{n}^{2}}$的对应项。
步骤 4:应用比较判别法
由于级数$\sum _{n=1}^{\infty }\dfrac {1}{{n}^{2}}$收敛,且级数$\sum _{n=1}^{\infty }(\sin \dfrac {1}{{n}^{2}})$的每一项都小于或等于级数$\sum _{n=1}^{\infty }\dfrac {1}{{n}^{2}}$的对应项,根据比较判别法,级数$\sum _{n=1}^{\infty }(\sin \dfrac {1}{{n}^{2}})$也收敛。