题目
[题目]已知 +y=1, 求 ^3+(y)^3+3xy 的值.
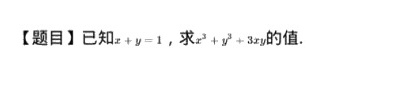
题目解答
答案
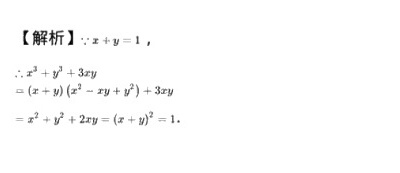
解析
考查要点:本题主要考查代数式的恒等变形能力,特别是对立方和公式及完全平方公式的灵活运用。
解题核心思路:
题目给出$x + y = 1$,要求计算$x^3 + y^3 + 3xy$的值。关键在于将高次项降次,利用立方和公式展开$x^3 + y^3$,再结合已知条件进行化简,最终转化为与$x + y$相关的表达式。
破题关键点:
- 应用立方和公式:将$x^3 + y^3$分解为$(x + y)(x^2 - xy + y^2)$。
- 代入已知条件:利用$x + y = 1$简化表达式。
- 合并同类项:将分解后的项与$3xy$结合,转化为完全平方形式。
步骤1:分解$x^3 + y^3$
根据立方和公式:
$x^3 + y^3 = (x + y)(x^2 - xy + y^2)$
代入已知条件$x + y = 1$,得:
$x^3 + y^3 = 1 \cdot (x^2 - xy + y^2) = x^2 - xy + y^2$
步骤2:代入原式并化简
原式为$x^3 + y^3 + 3xy$,代入分解后的结果:
$\begin{aligned}x^3 + y^3 + 3xy &= (x^2 - xy + y^2) + 3xy \\&= x^2 + y^2 + 2xy\end{aligned}$
步骤3:转化为完全平方形式
观察$x^2 + y^2 + 2xy$,可写成:
$x^2 + y^2 + 2xy = (x + y)^2$
代入$x + y = 1$,得:
$(x + y)^2 = 1^2 = 1$