题目
计算∫∫∫zdxdydz-|||-Ω, 其中Ω是由锥面∫∫∫zdxdydz-|||-Ω与平面z=h(R>0, h>0)所围成的闭区域.
计算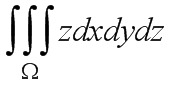 , 其中Ω是由锥面
, 其中Ω是由锥面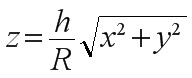 与平面z=h(R>0, h>0)所围成的闭区域.
与平面z=h(R>0, h>0)所围成的闭区域.
题目解答
答案
解 当0≤z≤h时, 过(0, 0, z)作平行于xOy面的平面, 截得立体Ω的截面为圆Dz: 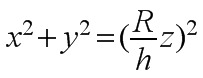 , 故Dz的半径为
, 故Dz的半径为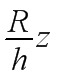 , 面积为
, 面积为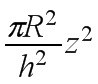 , 于是
, 于是
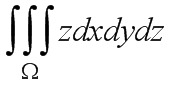 =
=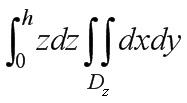
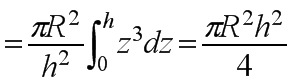 .
.
解析
考查要点:本题主要考查三重积分的计算,特别是利用截面法(柱坐标系)处理锥体区域的积分问题。
解题核心思路:
- 确定积分区域:闭区域Ω是由锥面$z=\dfrac{h}{R}\sqrt{x^2+y^2}$和平面$z=h$围成的圆锥体。
- 截面法简化积分:对于每个固定高度$z$,截面区域$D_z$是一个半径为$\dfrac{R}{h}z$的圆,面积为$\dfrac{\pi R^2}{h^2}z^2$。
- 转化为一重积分:将三重积分转化为对$z$的一重积分,被积函数为$z \cdot \text{截面面积}$。
破题关键点:
- 截面面积的表达式:通过锥面方程确定截面圆的半径,进而求出面积。
- 积分变量替换:利用$z$的范围$[0, h]$,将三重积分简化为对$z^3$的积分。
步骤1:确定截面区域
对于固定高度$z$,截面区域$D_z$由锥面方程$z=\dfrac{h}{R}\sqrt{x^2+y^2}$决定,解得$\sqrt{x^2+y^2}=\dfrac{R}{h}z$,即截面为半径$r=\dfrac{R}{h}z$的圆。
步骤2:计算截面面积
截面圆的面积为:
$S(z) = \pi r^2 = \pi \left( \dfrac{R}{h}z \right)^2 = \dfrac{\pi R^2}{h^2}z^2.$
步骤3:转化为一重积分
三重积分可表示为:
$\iiint_{\Omega} z \, dxdydz = \int_{0}^{h} z \cdot S(z) \, dz = \int_{0}^{h} z \cdot \dfrac{\pi R^2}{h^2}z^2 \, dz.$
步骤4:计算定积分
化简被积函数并积分:
$\int_{0}^{h} \dfrac{\pi R^2}{h^2} z^3 \, dz = \dfrac{\pi R^2}{h^2} \cdot \dfrac{h^4}{4} = \dfrac{\pi R^2 h^2}{4}.$