设函数f(x)可导,则极限f(x)( ).A. f(x) B. f(x) C. f(x) D. f(x)
设函数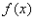 可导,则极限
可导,则极限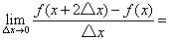 ( ).
( ).
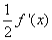
B.
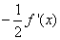
C.
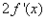
D.
题目解答
答案
C
【您的答案】 您未答题
【答案解析】
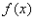 可导,则
可导,则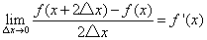
所以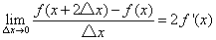
参见教材P71。
[单选题]
解析
考查要点:本题主要考查导数的定义及其极限形式的应用,需要学生理解导数的本质是函数在某点的瞬时变化率,并能灵活处理不同形式的增量表达式。
解题核心思路:
将题目中的极限表达式与导数的定义式进行对比,通过变量替换或调整分母的方式,将原式转化为标准导数形式,从而直接得出结果。
破题关键点:
- 识别导数定义的变形:分子中的增量为$2\Delta x$,而分母是$\Delta x$,需通过调整变量或系数,使其符合$f'(x)$的标准极限形式。
- 系数处理:通过将分子和分母同时乘以系数,或引入新变量$h=2\Delta x$,将原式转化为$f'(x)$的倍数。
步骤1:对比导数定义
导数的定义为:
$f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}.$
题目中的极限形式为:
$\lim_{\Delta x \to 0} \frac{f(x+2\Delta x) - f(x)}{\Delta x}.$
观察发现,分子中的增量是$2\Delta x$,而分母是$\Delta x$,需调整使其匹配导数定义。
步骤2:变量替换
令$h = 2\Delta x$,则当$\Delta x \to 0$时,$h \to 0$,且$\Delta x = \frac{h}{2}$。将原式改写为:
$\lim_{h \to 0} \frac{f(x+h) - f(x)}{\frac{h}{2}} = \lim_{h \to 0} \frac{2[f(x+h) - f(x)]}{h} = 2f'(x).$
步骤3:直接调整分母
原式可拆分为:
$\lim_{\Delta x \to 0} \frac{f(x+2\Delta x) - f(x)}{2\Delta x} \cdot 2.$
根据导数定义,$\lim_{\Delta x \to 0} \frac{f(x+2\Delta x) - f(x)}{2\Delta x} = f'(x)$,因此原式等于$2f'(x)$。