题目
16.分别由下列条件求解析函数 f(z)=u+iv 。-|||-(1) =(x)^2+xy-(y)^2 ,-|||-f(i)=-1+i ;-|||-(2) =(e)^x(xcos y-ysin y) ,-|||-f(0)=0 ;-|||-(3) =dfrac (y)({x)^2+(y)^2} ,-|||-f(2)=0 。
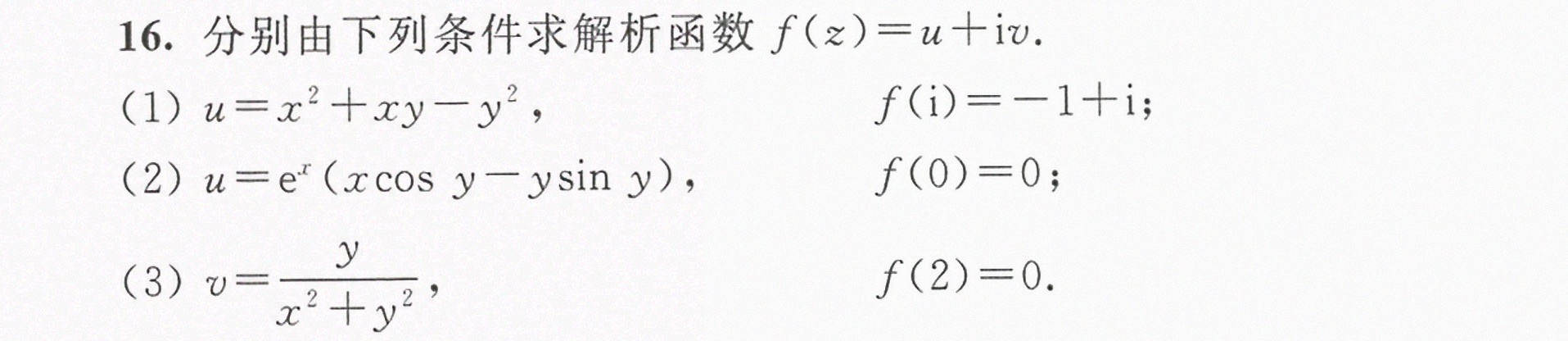
题目解答
答案
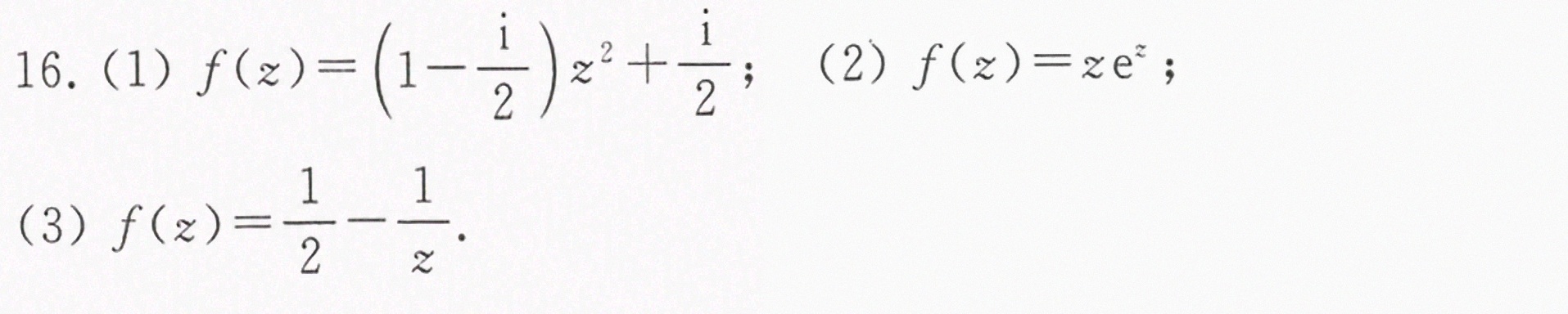
解析
(1) 步骤 1:确定 v 的形式
根据给定的 u,利用柯西-黎曼方程 $\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}$ 和 $\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$,可以求出 v 的形式。
步骤 2:计算 v
计算 $\frac{\partial u}{\partial x} = 2x + y$ 和 $\frac{\partial u}{\partial y} = x - 2y$,然后根据柯西-黎曼方程求出 v。
步骤 3:确定 f(z)
将 u 和 v 代入 f(z) = u + iv,然后利用给定的条件 f(i) = -1 + i 来确定常数项。
(2) 步骤 1:确定 v 的形式
根据给定的 u,利用柯西-黎曼方程 $\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}$ 和 $\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$,可以求出 v 的形式。
步骤 2:计算 v
计算 $\frac{\partial u}{\partial x} = {e}^{x}(x\cos y - y\sin y + \cos y)$ 和 $\frac{\partial u}{\partial y} = {e}^{x}(-x\sin y - \sin y - y\cos y)$,然后根据柯西-黎曼方程求出 v。
步骤 3:确定 f(z)
将 u 和 v 代入 f(z) = u + iv,然后利用给定的条件 f(0) = 0 来确定常数项。
(3) 步骤 1:确定 u 的形式
根据给定的 v,利用柯西-黎曼方程 $\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}$ 和 $\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$,可以求出 u 的形式。
步骤 2:计算 u
计算 $\frac{\partial v}{\partial y} = \frac{{x}^{2}-{y}^{2}}{({x}^{2}+{y}^{2})^{2}}$ 和 $\frac{\partial v}{\partial x} = \frac{-2xy}{({x}^{2}+{y}^{2})^{2}}$,然后根据柯西-黎曼方程求出 u。
步骤 3:确定 f(z)
将 u 和 v 代入 f(z) = u + iv,然后利用给定的条件 f(2) = 0 来确定常数项。
根据给定的 u,利用柯西-黎曼方程 $\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}$ 和 $\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$,可以求出 v 的形式。
步骤 2:计算 v
计算 $\frac{\partial u}{\partial x} = 2x + y$ 和 $\frac{\partial u}{\partial y} = x - 2y$,然后根据柯西-黎曼方程求出 v。
步骤 3:确定 f(z)
将 u 和 v 代入 f(z) = u + iv,然后利用给定的条件 f(i) = -1 + i 来确定常数项。
(2) 步骤 1:确定 v 的形式
根据给定的 u,利用柯西-黎曼方程 $\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}$ 和 $\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$,可以求出 v 的形式。
步骤 2:计算 v
计算 $\frac{\partial u}{\partial x} = {e}^{x}(x\cos y - y\sin y + \cos y)$ 和 $\frac{\partial u}{\partial y} = {e}^{x}(-x\sin y - \sin y - y\cos y)$,然后根据柯西-黎曼方程求出 v。
步骤 3:确定 f(z)
将 u 和 v 代入 f(z) = u + iv,然后利用给定的条件 f(0) = 0 来确定常数项。
(3) 步骤 1:确定 u 的形式
根据给定的 v,利用柯西-黎曼方程 $\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}$ 和 $\frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x}$,可以求出 u 的形式。
步骤 2:计算 u
计算 $\frac{\partial v}{\partial y} = \frac{{x}^{2}-{y}^{2}}{({x}^{2}+{y}^{2})^{2}}$ 和 $\frac{\partial v}{\partial x} = \frac{-2xy}{({x}^{2}+{y}^{2})^{2}}$,然后根据柯西-黎曼方程求出 u。
步骤 3:确定 f(z)
将 u 和 v 代入 f(z) = u + iv,然后利用给定的条件 f(2) = 0 来确定常数项。