题目
过直线_(1):dfrac (x-1)(1)=dfrac (y-2)(0)=dfrac (z-3)(-1)-|||-__ __且平行于直线_(1):dfrac (x-1)(1)=dfrac (y-2)(0)=dfrac (z-3)(-1)-|||-__ __的平面的方程为_______________.
过直线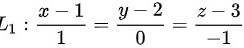 且平行于直线
且平行于直线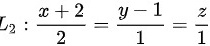 的平面的方程为_______________.
的平面的方程为_______________.
题目解答
答案
解:设所求平面为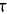 ,其法向量为
,其法向量为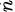 ,由题设知,
,由题设知,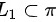 ,故
,故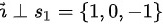 ,又
,又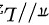 ,于是
,于是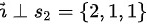 ,取平面
,取平面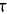 的法向量为
的法向量为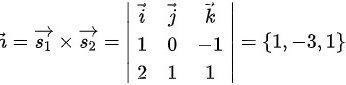 又因为
又因为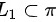 ,所以点
,所以点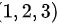 也在
也在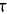 上,故根据点法式得到平面方程为
上,故根据点法式得到平面方程为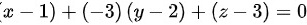 ,即
,即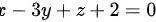
答案: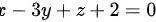
解析
步骤 1:确定直线${l}_{1}$的方向向量
直线${l}_{1}:\dfrac {x-1}{1}=\dfrac {y-2}{0}=\dfrac {z-3}{-1}$的方向向量为${S}_{1}=\{ 1,0,-1\} $。
步骤 2:确定直线${l}_{2}$的方向向量
直线${l}_{2}:\dfrac {x+2}{2}=\dfrac {y-1}{1}=\dfrac {z}{1}$的方向向量为${S}_{2}=\{ 2,1,1\} $。
步骤 3:求平面的法向量
因为所求平面平行于直线${l}_{2}$,所以平面的法向量$\overrightarrow {n}$垂直于${S}_{2}$。同时,因为直线${l}_{1}$在所求平面上,所以$\overrightarrow {n}$也垂直于${S}_{1}$。因此,$\overrightarrow {n}$可以由${S}_{1}$和${S}_{2}$的叉乘得到。
步骤 4:计算叉乘
$\overrightarrow {n}={S}_{1}\times {S}_{2}=\begin{vmatrix} i & j & k \\ 1 & 0 & -1 \\ 2 & 1 & 1 \end{vmatrix} =\{ 1\times 1-(-1)\times 1,(-1)\times 2-1\times 1,1\times 1-0\times 2\} =\{ 2,-3,1\} $。
步骤 5:确定平面方程
因为直线${l}_{1}$在所求平面上,所以点(1,2,3)也在平面上。根据点法式,平面方程为$(x-1)+(-3)(y-2)+(z-3)=0$,即$x-3y+z+2=0$。
直线${l}_{1}:\dfrac {x-1}{1}=\dfrac {y-2}{0}=\dfrac {z-3}{-1}$的方向向量为${S}_{1}=\{ 1,0,-1\} $。
步骤 2:确定直线${l}_{2}$的方向向量
直线${l}_{2}:\dfrac {x+2}{2}=\dfrac {y-1}{1}=\dfrac {z}{1}$的方向向量为${S}_{2}=\{ 2,1,1\} $。
步骤 3:求平面的法向量
因为所求平面平行于直线${l}_{2}$,所以平面的法向量$\overrightarrow {n}$垂直于${S}_{2}$。同时,因为直线${l}_{1}$在所求平面上,所以$\overrightarrow {n}$也垂直于${S}_{1}$。因此,$\overrightarrow {n}$可以由${S}_{1}$和${S}_{2}$的叉乘得到。
步骤 4:计算叉乘
$\overrightarrow {n}={S}_{1}\times {S}_{2}=\begin{vmatrix} i & j & k \\ 1 & 0 & -1 \\ 2 & 1 & 1 \end{vmatrix} =\{ 1\times 1-(-1)\times 1,(-1)\times 2-1\times 1,1\times 1-0\times 2\} =\{ 2,-3,1\} $。
步骤 5:确定平面方程
因为直线${l}_{1}$在所求平面上,所以点(1,2,3)也在平面上。根据点法式,平面方程为$(x-1)+(-3)(y-2)+(z-3)=0$,即$x-3y+z+2=0$。