题目
函数(x)=dfrac (ln |x|)(sqrt {1-{x)^2}}的定义域是 A(x)=dfrac (ln |x|)(sqrt {1-{x)^2}} B ( -1 , 1 ) C ( -1 , 0 ) D ( 0 , 1 )
函数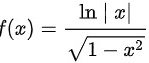
的定义域是
A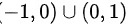
B ( -1 , 1 ) C ( -1 , 0 ) D ( 0 , 1 )
题目解答
答案
解：
对于函数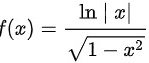
分母的被开方数大于零。即
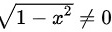且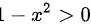
解得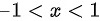
分子的幂保证大于零，即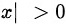
解得x≠0
最后x的取值范围是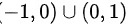
答案选A
解析
步骤 1：确定分母的定义域
分母$\sqrt {1-{x}^{2}}$要求$1-{x}^{2} > 0$，即$x^2 < 1$，解得$-1 < x < 1$。
步骤 2：确定分子的定义域
分子$\ln |x|$要求$|x| > 0$，即$x \neq 0$。
步骤 3：合并定义域
结合步骤1和步骤2，函数$f(x)$的定义域为$(-1,0)\cup (0,1)$。
分母$\sqrt {1-{x}^{2}}$要求$1-{x}^{2} > 0$，即$x^2 < 1$，解得$-1 < x < 1$。
步骤 2：确定分子的定义域
分子$\ln |x|$要求$|x| > 0$，即$x \neq 0$。
步骤 3：合并定义域
结合步骤1和步骤2，函数$f(x)$的定义域为$(-1,0)\cup (0,1)$。