题目
|(x)^2-3x+2|geqslant 1-|||-__
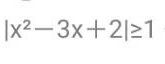
题目解答
答案
解析
步骤 1:分析绝对值不等式
绝对值不等式 $|{x}^{2}-3x+2|\geqslant 1$ 可以转化为两个不等式:${x}^{2}-3x+2\geqslant 1$ 和 ${x}^{2}-3x+2\leqslant -1$。
步骤 2:解第一个不等式
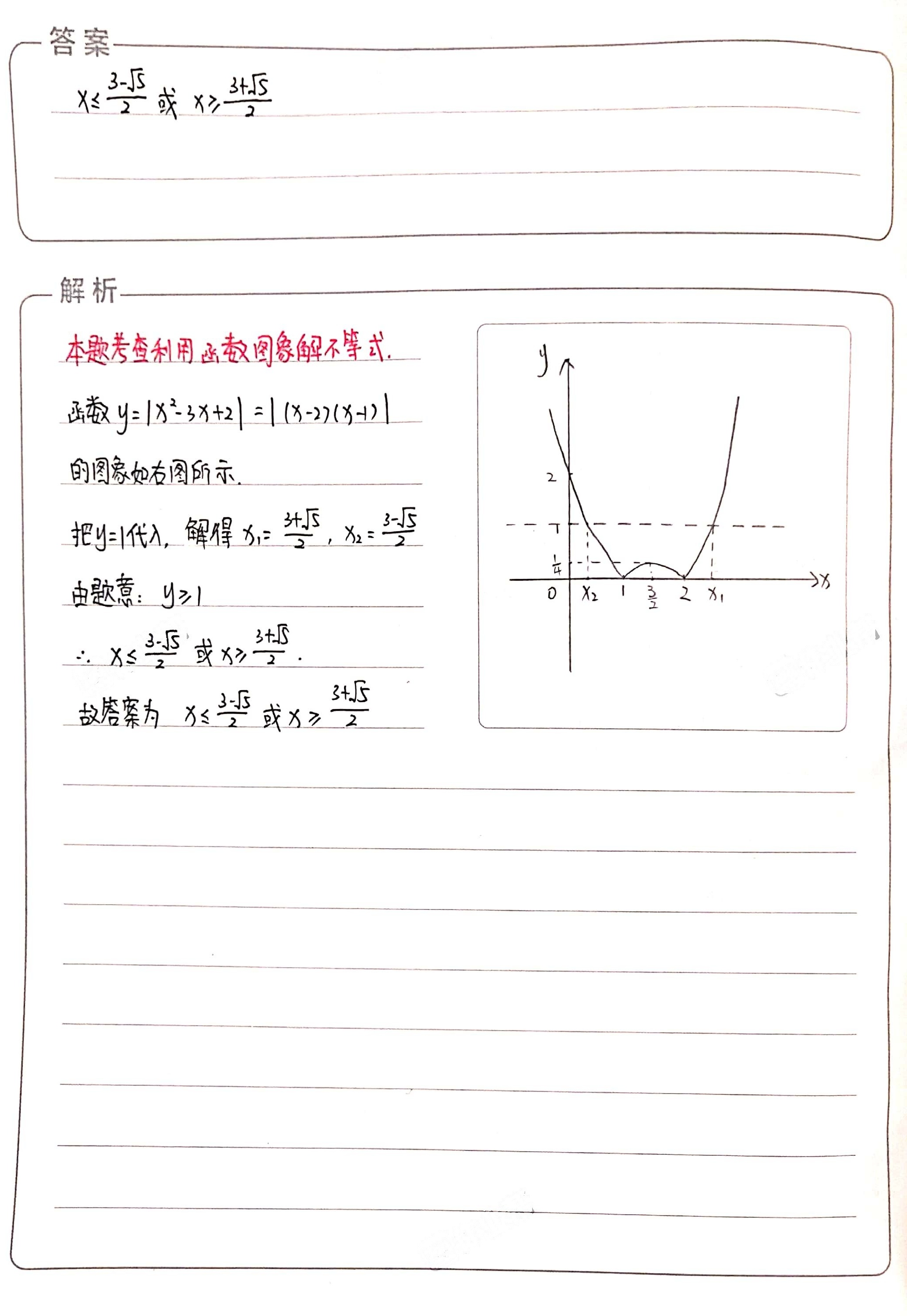
解不等式 ${x}^{2}-3x+2\geqslant 1$,即 ${x}^{2}-3x+1\geqslant 0$。求解该不等式,首先求解对应的方程 ${x}^{2}-3x+1=0$,得到 $x=\frac{3\pm\sqrt{5}}{2}$。因此,不等式的解集为 $x\leqslant \frac{3-\sqrt{5}}{2}$ 或 $x\geqslant \frac{3+\sqrt{5}}{2}$。
步骤 3:解第二个不等式
解不等式 ${x}^{2}-3x+2\leqslant -1$,即 ${x}^{2}-3x+3\leqslant 0$。求解该不等式,首先求解对应的方程 ${x}^{2}-3x+3=0$,但该方程无实数解,因此不等式 ${x}^{2}-3x+3\leqslant 0$ 无解。
步骤 4:合并解集
将步骤 2 和步骤 3 的解集合并,得到最终解集为 $x\leqslant \frac{3-\sqrt{5}}{2}$ 或 $x\geqslant \frac{3+\sqrt{5}}{2}$。
绝对值不等式 $|{x}^{2}-3x+2|\geqslant 1$ 可以转化为两个不等式:${x}^{2}-3x+2\geqslant 1$ 和 ${x}^{2}-3x+2\leqslant -1$。
步骤 2:解第一个不等式
解不等式 ${x}^{2}-3x+2\geqslant 1$,即 ${x}^{2}-3x+1\geqslant 0$。求解该不等式,首先求解对应的方程 ${x}^{2}-3x+1=0$,得到 $x=\frac{3\pm\sqrt{5}}{2}$。因此,不等式的解集为 $x\leqslant \frac{3-\sqrt{5}}{2}$ 或 $x\geqslant \frac{3+\sqrt{5}}{2}$。
步骤 3:解第二个不等式
解不等式 ${x}^{2}-3x+2\leqslant -1$,即 ${x}^{2}-3x+3\leqslant 0$。求解该不等式,首先求解对应的方程 ${x}^{2}-3x+3=0$,但该方程无实数解,因此不等式 ${x}^{2}-3x+3\leqslant 0$ 无解。
步骤 4:合并解集
将步骤 2 和步骤 3 的解集合并,得到最终解集为 $x\leqslant \frac{3-\sqrt{5}}{2}$ 或 $x\geqslant \frac{3+\sqrt{5}}{2}$。