题目
3.计算下列二重积分:-|||-(2) iint xsqrt (y)dxdy, 其中D是由抛物线 =sqrt (x) 和 =(x)^2 所围成的闭区域.
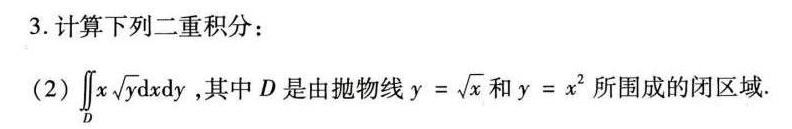
题目解答
答案
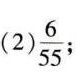
解析
步骤 1:确定积分区域D
首先,我们需要确定积分区域D。D是由抛物线 $y=\sqrt{x}$ 和 $y=x^2$ 所围成的闭区域。为了找到这两个曲线的交点,我们解方程 $\sqrt{x} = x^2$。解得 $x=0$ 和 $x=1$。因此,积分区域D在x轴上的范围是0到1。
步骤 2:设置积分
根据步骤1,我们可以设置二重积分的上下限。由于积分区域D在x轴上的范围是0到1,我们可以将二重积分写为:
$$
\int_{0}^{1} \int_{x^2}^{\sqrt{x}} x\sqrt{y} \, dy \, dx
$$
步骤 3:计算内层积分
首先计算内层积分,即对y的积分:
$$
\int_{x^2}^{\sqrt{x}} x\sqrt{y} \, dy
$$
将 $x\sqrt{y}$ 看作y的函数,积分得到:
$$
\int_{x^2}^{\sqrt{x}} x\sqrt{y} \, dy = x \int_{x^2}^{\sqrt{x}} y^{1/2} \, dy = x \left[ \frac{2}{3} y^{3/2} \right]_{x^2}^{\sqrt{x}} = x \left( \frac{2}{3} (\sqrt{x})^{3/2} - \frac{2}{3} (x^2)^{3/2} \right)
$$
$$
= x \left( \frac{2}{3} x^{3/4} - \frac{2}{3} x^3 \right) = \frac{2}{3} x^{7/4} - \frac{2}{3} x^4
$$
步骤 4:计算外层积分
接下来计算外层积分,即对x的积分:
$$
\int_{0}^{1} \left( \frac{2}{3} x^{7/4} - \frac{2}{3} x^4 \right) \, dx
$$
分别对每一项积分:
$$
\int_{0}^{1} \frac{2}{3} x^{7/4} \, dx = \frac{2}{3} \left[ \frac{4}{11} x^{11/4} \right]_{0}^{1} = \frac{2}{3} \cdot \frac{4}{11} = \frac{8}{33}
$$
$$
\int_{0}^{1} \frac{2}{3} x^4 \, dx = \frac{2}{3} \left[ \frac{1}{5} x^5 \right]_{0}^{1} = \frac{2}{3} \cdot \frac{1}{5} = \frac{2}{15}
$$
因此,外层积分的结果为:
$$
\frac{8}{33} - \frac{2}{15} = \frac{40}{165} - \frac{22}{165} = \frac{18}{165} = \frac{6}{55}
$$
首先,我们需要确定积分区域D。D是由抛物线 $y=\sqrt{x}$ 和 $y=x^2$ 所围成的闭区域。为了找到这两个曲线的交点,我们解方程 $\sqrt{x} = x^2$。解得 $x=0$ 和 $x=1$。因此,积分区域D在x轴上的范围是0到1。
步骤 2:设置积分
根据步骤1,我们可以设置二重积分的上下限。由于积分区域D在x轴上的范围是0到1,我们可以将二重积分写为:
$$
\int_{0}^{1} \int_{x^2}^{\sqrt{x}} x\sqrt{y} \, dy \, dx
$$
步骤 3:计算内层积分
首先计算内层积分,即对y的积分:
$$
\int_{x^2}^{\sqrt{x}} x\sqrt{y} \, dy
$$
将 $x\sqrt{y}$ 看作y的函数,积分得到:
$$
\int_{x^2}^{\sqrt{x}} x\sqrt{y} \, dy = x \int_{x^2}^{\sqrt{x}} y^{1/2} \, dy = x \left[ \frac{2}{3} y^{3/2} \right]_{x^2}^{\sqrt{x}} = x \left( \frac{2}{3} (\sqrt{x})^{3/2} - \frac{2}{3} (x^2)^{3/2} \right)
$$
$$
= x \left( \frac{2}{3} x^{3/4} - \frac{2}{3} x^3 \right) = \frac{2}{3} x^{7/4} - \frac{2}{3} x^4
$$
步骤 4:计算外层积分
接下来计算外层积分,即对x的积分:
$$
\int_{0}^{1} \left( \frac{2}{3} x^{7/4} - \frac{2}{3} x^4 \right) \, dx
$$
分别对每一项积分:
$$
\int_{0}^{1} \frac{2}{3} x^{7/4} \, dx = \frac{2}{3} \left[ \frac{4}{11} x^{11/4} \right]_{0}^{1} = \frac{2}{3} \cdot \frac{4}{11} = \frac{8}{33}
$$
$$
\int_{0}^{1} \frac{2}{3} x^4 \, dx = \frac{2}{3} \left[ \frac{1}{5} x^5 \right]_{0}^{1} = \frac{2}{3} \cdot \frac{1}{5} = \frac{2}{15}
$$
因此,外层积分的结果为:
$$
\frac{8}{33} - \frac{2}{15} = \frac{40}{165} - \frac{22}{165} = \frac{18}{165} = \frac{6}{55}
$$