题目
二维随机 变量 ( X , Y ) 的联合概率密度为f(x,y)= ) 1,0leqslant xleqslant 1,0leqslant yleqslant 2x 0, xin R .；
二维随机 变量 ( X , Y ) 的联合概率密度为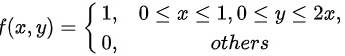
(1)求边缘概率密度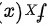
，
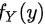并判断 X 与 Y 是否独立 ;
（2） 计算 X 与 Y 的协方差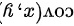
；
题目解答
答案
解：（1）根据边缘概率密度函数公式
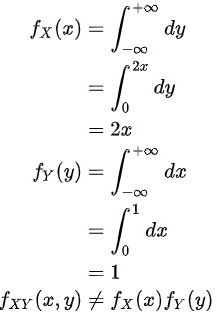
∴X 与 Y 不相互独立
（2）
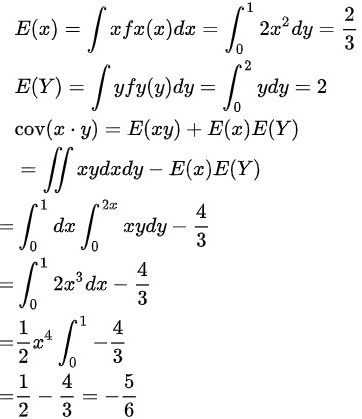
解析
步骤 1：求边缘概率密度$f(x)$
边缘概率密度$f(x)$是通过将联合概率密度函数$f(x,y)$在$y$的范围内积分得到的。根据题目中的联合概率密度函数$f(x,y)$，我们有：
$$
f(x) = \int_{-\infty}^{+\infty} f(x,y) dy = \int_{0}^{2x} 1 dy = 2x
$$
其中，$0 \leq x \leq 1$，在其他情况下$f(x) = 0$。
步骤 2：求边缘概率密度${f}_{y}(y)$
边缘概率密度${f}_{y}(y)$是通过将联合概率密度函数$f(x,y)$在$x$的范围内积分得到的。根据题目中的联合概率密度函数$f(x,y)$，我们有：
$$
{f}_{y}(y) = \int_{-\infty}^{+\infty} f(x,y) dx = \int_{y/2}^{1} 1 dx = 1 - \frac{y}{2}
$$
其中，$0 \leq y \leq 2$，在其他情况下${f}_{y}(y) = 0$。
步骤 3：判断 X 与 Y 是否独立
两个随机变量X和Y独立的充分必要条件是它们的联合概率密度函数等于它们边缘概率密度函数的乘积，即$f(x,y) = f(x) \cdot {f}_{y}(y)$。根据题目中的联合概率密度函数$f(x,y)$和我们计算出的边缘概率密度$f(x)$和${f}_{y}(y)$，我们有：
$$
f(x,y) = 1 \neq 2x \cdot (1 - \frac{y}{2}) = f(x) \cdot {f}_{y}(y)
$$
因此，X与Y不相互独立。
步骤 4：计算 X 与 Y 的协方差$COV(x,y)$
协方差$COV(x,y)$的计算公式为$COV(x,y) = E(xy) - E(x)E(y)$，其中$E(xy)$是随机变量$xy$的期望值，$E(x)$和$E(y)$分别是随机变量$x$和$y$的期望值。根据题目中的联合概率密度函数$f(x,y)$，我们有：
$$
E(x) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} x f(x,y) dx dy = \int_{0}^{1} \int_{0}^{2x} x dy dx = \int_{0}^{1} 2x^2 dx = \frac{2}{3}
$$
$$
E(y) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} y f(x,y) dx dy = \int_{0}^{1} \int_{0}^{2x} y dy dx = \int_{0}^{1} x^2 dx = \frac{1}{3}
$$
$$
E(xy) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} xy f(x,y) dx dy = \int_{0}^{1} \int_{0}^{2x} xy dy dx = \int_{0}^{1} x^3 dx = \frac{1}{4}
$$
因此，$COV(x,y) = E(xy) - E(x)E(y) = \frac{1}{4} - \frac{2}{3} \cdot \frac{1}{3} = \frac{1}{4} - \frac{2}{9} = \frac{9}{36} - \frac{8}{36} = \frac{1}{36}$。
边缘概率密度$f(x)$是通过将联合概率密度函数$f(x,y)$在$y$的范围内积分得到的。根据题目中的联合概率密度函数$f(x,y)$，我们有：
$$
f(x) = \int_{-\infty}^{+\infty} f(x,y) dy = \int_{0}^{2x} 1 dy = 2x
$$
其中，$0 \leq x \leq 1$，在其他情况下$f(x) = 0$。
步骤 2：求边缘概率密度${f}_{y}(y)$
边缘概率密度${f}_{y}(y)$是通过将联合概率密度函数$f(x,y)$在$x$的范围内积分得到的。根据题目中的联合概率密度函数$f(x,y)$，我们有：
$$
{f}_{y}(y) = \int_{-\infty}^{+\infty} f(x,y) dx = \int_{y/2}^{1} 1 dx = 1 - \frac{y}{2}
$$
其中，$0 \leq y \leq 2$，在其他情况下${f}_{y}(y) = 0$。
步骤 3：判断 X 与 Y 是否独立
两个随机变量X和Y独立的充分必要条件是它们的联合概率密度函数等于它们边缘概率密度函数的乘积，即$f(x,y) = f(x) \cdot {f}_{y}(y)$。根据题目中的联合概率密度函数$f(x,y)$和我们计算出的边缘概率密度$f(x)$和${f}_{y}(y)$，我们有：
$$
f(x,y) = 1 \neq 2x \cdot (1 - \frac{y}{2}) = f(x) \cdot {f}_{y}(y)
$$
因此，X与Y不相互独立。
步骤 4：计算 X 与 Y 的协方差$COV(x,y)$
协方差$COV(x,y)$的计算公式为$COV(x,y) = E(xy) - E(x)E(y)$，其中$E(xy)$是随机变量$xy$的期望值，$E(x)$和$E(y)$分别是随机变量$x$和$y$的期望值。根据题目中的联合概率密度函数$f(x,y)$，我们有：
$$
E(x) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} x f(x,y) dx dy = \int_{0}^{1} \int_{0}^{2x} x dy dx = \int_{0}^{1} 2x^2 dx = \frac{2}{3}
$$
$$
E(y) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} y f(x,y) dx dy = \int_{0}^{1} \int_{0}^{2x} y dy dx = \int_{0}^{1} x^2 dx = \frac{1}{3}
$$
$$
E(xy) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} xy f(x,y) dx dy = \int_{0}^{1} \int_{0}^{2x} xy dy dx = \int_{0}^{1} x^3 dx = \frac{1}{4}
$$
因此，$COV(x,y) = E(xy) - E(x)E(y) = \frac{1}{4} - \frac{2}{3} \cdot \frac{1}{3} = \frac{1}{4} - \frac{2}{9} = \frac{9}{36} - \frac{8}{36} = \frac{1}{36}$。