题目
六、计算曲线积分 int (2(x)^2-(y)^2+(x)^2(e)^3y)dx+((x)^3(e)^3y-2xy-2(y)^2)dy, 其中L为椭圆-|||-^2+dfrac ({y)^2}(9)=1 上从点 A(-1,0) 经第二象限至点B(0,3)的弧段.
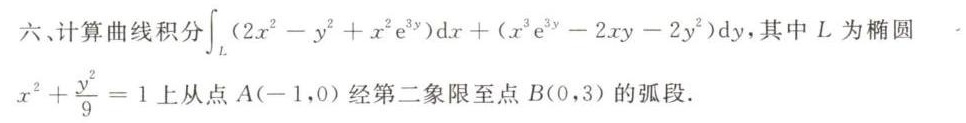
题目解答
答案
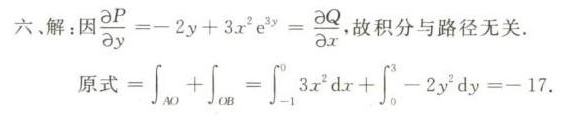
解析
步骤 1:验证积分与路径无关
首先,我们验证积分与路径无关。为此,我们需要检查 $\dfrac {\partial P}{\partial y}$ 和 $\dfrac {\partial Q}{\partial x}$ 是否相等,其中 $P = 2{x}^{2}-{y}^{2}+{x}^{2}{e}^{3y}$ 和 $Q = {x}^{2}{e}^{3y}-2xy-2{y}^{2}$。
计算 $\dfrac {\partial P}{\partial y}$ 和 $\dfrac {\partial Q}{\partial x}$:
$$\dfrac {\partial P}{\partial y} = -2y + 3{x}^{2}{e}^{3y}$$
$$\dfrac {\partial Q}{\partial x} = 2x{e}^{3y} - 2y$$
由于 $\dfrac {\partial P}{\partial y} = \dfrac {\partial Q}{\partial x}$,积分与路径无关。
步骤 2:选择路径
由于积分与路径无关,我们可以选择任意路径从点A(-1,0)到点B(0,3)。这里,我们选择分段路径,先沿x轴从A到原点O(0,0),再沿y轴从原点O到B。
步骤 3:计算积分
计算沿x轴从A到O的积分:
$$\int_{A}^{O} (2{x}^{2}-{y}^{2}+{x}^{2}{e}^{3y})dx = \int_{-1}^{0} (2{x}^{2}+{x}^{2})dx = \int_{-1}^{0} 3{x}^{2}dx = {x}^{3}|_{-1}^{0} = 0 - (-1) = 1$$
计算沿y轴从O到B的积分:
$$\int_{O}^{B} ({x}^{2}{e}^{3y}-2xy-2{y}^{2})dy = \int_{0}^{3} (-2{y}^{2})dy = -\dfrac {2}{3}{y}^{3}|_{0}^{3} = -\dfrac {2}{3}(27) = -18$$
将两个积分结果相加:
$$1 + (-18) = -17$$
首先,我们验证积分与路径无关。为此,我们需要检查 $\dfrac {\partial P}{\partial y}$ 和 $\dfrac {\partial Q}{\partial x}$ 是否相等,其中 $P = 2{x}^{2}-{y}^{2}+{x}^{2}{e}^{3y}$ 和 $Q = {x}^{2}{e}^{3y}-2xy-2{y}^{2}$。
计算 $\dfrac {\partial P}{\partial y}$ 和 $\dfrac {\partial Q}{\partial x}$:
$$\dfrac {\partial P}{\partial y} = -2y + 3{x}^{2}{e}^{3y}$$
$$\dfrac {\partial Q}{\partial x} = 2x{e}^{3y} - 2y$$
由于 $\dfrac {\partial P}{\partial y} = \dfrac {\partial Q}{\partial x}$,积分与路径无关。
步骤 2:选择路径
由于积分与路径无关,我们可以选择任意路径从点A(-1,0)到点B(0,3)。这里,我们选择分段路径,先沿x轴从A到原点O(0,0),再沿y轴从原点O到B。
步骤 3:计算积分
计算沿x轴从A到O的积分:
$$\int_{A}^{O} (2{x}^{2}-{y}^{2}+{x}^{2}{e}^{3y})dx = \int_{-1}^{0} (2{x}^{2}+{x}^{2})dx = \int_{-1}^{0} 3{x}^{2}dx = {x}^{3}|_{-1}^{0} = 0 - (-1) = 1$$
计算沿y轴从O到B的积分:
$$\int_{O}^{B} ({x}^{2}{e}^{3y}-2xy-2{y}^{2})dy = \int_{0}^{3} (-2{y}^{2})dy = -\dfrac {2}{3}{y}^{3}|_{0}^{3} = -\dfrac {2}{3}(27) = -18$$
将两个积分结果相加:
$$1 + (-18) = -17$$