计算下列极限lim _(narrow infty )dfrac (1)({n)^2}(sqrt (n)+sqrt (2n)+... +sqrt ({n)^2})
计算下列极限
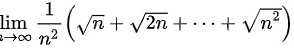
题目解答
答案
由定积分的定义
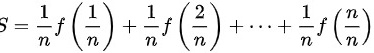
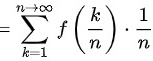
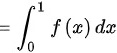
∴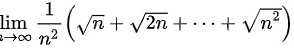
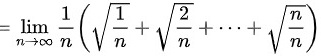
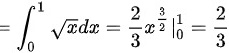
解析
考查要点:本题主要考查利用定积分定义求解数列极限的能力,需要将求和式转化为积分形式。
解题核心思路:
将求和式中的每一项$\sqrt{kn}$变形为$n \cdot \sqrt{\dfrac{k}{n}}$,从而将原式转化为$\dfrac{1}{n} \sum \sqrt{\dfrac{k}{n}}$,进而应用定积分的定义求解。
破题关键点:
- 提取公因子:将$\sqrt{kn}$拆分为$n \cdot \sqrt{\dfrac{k}{n}}$,使表达式符合积分定义的结构。
- 识别积分元素:$\dfrac{1}{n}$对应积分中的小区间宽度$\Delta x$,$\sqrt{\dfrac{k}{n}}$对应函数值$f(x)$。
将原式变形为积分形式:
$\begin{aligned}\lim _{n\rightarrow \infty }\dfrac {1}{{n}^{2}}(\sqrt {n}+\sqrt {2n}+\cdots +\sqrt {{n}^{2}}) &= \lim _{n\rightarrow \infty }\dfrac {1}{n^{2}} \sum_{k=1}^{n} \sqrt{kn} \\&= \lim _{n\rightarrow \infty }\dfrac {1}{n^{2}} \sum_{k=1}^{n} \left( n \cdot \sqrt{\dfrac{k}{n}} \right) \quad \text{(提取公因子$n$)} \\&= \lim _{n\rightarrow \infty }\dfrac {1}{n} \sum_{k=1}^{n} \sqrt{\dfrac{k}{n}} \quad \text{(化简后)} \\&= \int_{0}^{1} \sqrt{x} \, dx \quad \text{(应用定积分定义)} \\&= \dfrac{2}{3} x^{\dfrac{3}{2}} \Big|_{0}^{1} = \dfrac{2}{3}.\end{aligned}$