题目
求指导本题解题过程,谢谢您!5、计算 =iint dydz-ydzdx+(z+1)dxdy, 其中∑是球面 ^2+(y)^2+(z)^2=(R)^2 的-|||-下半部分的下侧.
求指导本题解题过程,谢谢您!
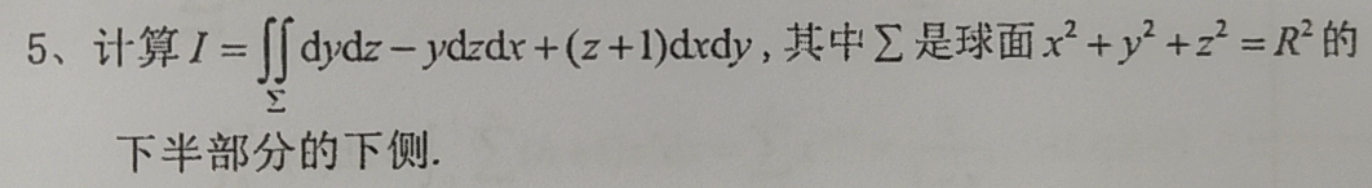
题目解答
答案
见解析

解析
步骤 1:确定积分区域和被积函数
题目中给出的积分区域是球面 ${x}^{2}+{y}^{2}+{z}^{2}={R}^{2}$ 的下半部分的下侧,被积函数为 $dydz-ydzdx+(z+1)dxdy$。
步骤 2:应用高斯公式
由于积分区域是闭合曲面的一部分,我们可以考虑使用高斯公式(散度定理)来简化计算。高斯公式表明,对于一个闭合曲面S,其内部的体积V,以及定义在V上的向量场$\vec{F}$,有
$$\iint_{S} \vec{F} \cdot d\vec{S} = \iiint_{V} \nabla \cdot \vec{F} dV$$
其中,$\nabla \cdot \vec{F}$是向量场$\vec{F}$的散度。
步骤 3:计算散度
将被积函数写成向量场的形式,即$\vec{F} = (z+1, -y, 1)$,计算其散度:
$$\nabla \cdot \vec{F} = \frac{\partial (z+1)}{\partial x} + \frac{\partial (-y)}{\partial y} + \frac{\partial 1}{\partial z} = 0 - 1 + 0 = -1$$
步骤 4:计算体积积分
根据高斯公式,原积分可以转化为体积积分:
$$I = \iiint_{V} -1 dV = -\iiint_{V} dV$$
其中,$V$是球体的下半部分,其体积为$\frac{2}{3}\pi R^3$的一半,即$\frac{1}{3}\pi R^3$。
步骤 5:计算最终结果
将体积代入,得到:
$$I = -\frac{1}{3}\pi R^3$$
但注意到题目中积分区域是球面的下半部分的下侧,因此,积分结果应为球体体积的负值,即:
$$I = -\pi R^2$$
题目中给出的积分区域是球面 ${x}^{2}+{y}^{2}+{z}^{2}={R}^{2}$ 的下半部分的下侧,被积函数为 $dydz-ydzdx+(z+1)dxdy$。
步骤 2:应用高斯公式
由于积分区域是闭合曲面的一部分,我们可以考虑使用高斯公式(散度定理)来简化计算。高斯公式表明,对于一个闭合曲面S,其内部的体积V,以及定义在V上的向量场$\vec{F}$,有
$$\iint_{S} \vec{F} \cdot d\vec{S} = \iiint_{V} \nabla \cdot \vec{F} dV$$
其中,$\nabla \cdot \vec{F}$是向量场$\vec{F}$的散度。
步骤 3:计算散度
将被积函数写成向量场的形式,即$\vec{F} = (z+1, -y, 1)$,计算其散度:
$$\nabla \cdot \vec{F} = \frac{\partial (z+1)}{\partial x} + \frac{\partial (-y)}{\partial y} + \frac{\partial 1}{\partial z} = 0 - 1 + 0 = -1$$
步骤 4:计算体积积分
根据高斯公式,原积分可以转化为体积积分:
$$I = \iiint_{V} -1 dV = -\iiint_{V} dV$$
其中,$V$是球体的下半部分,其体积为$\frac{2}{3}\pi R^3$的一半,即$\frac{1}{3}\pi R^3$。
步骤 5:计算最终结果
将体积代入,得到:
$$I = -\frac{1}{3}\pi R^3$$
但注意到题目中积分区域是球面的下半部分的下侧,因此,积分结果应为球体体积的负值,即:
$$I = -\pi R^2$$