题目
函数自变量在一点处的改变量就等于自变量在这点处的微分。（ ）A 正确B 错误
函数自变量在一点处的改变量就等于自变量在这点处的微分。（ ）
A 正确
B 错误
题目解答
答案
对于增量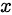
来说，它的高阶无穷小就是0，看定义式：
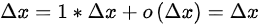,因此，函数自变量在一点处的改变量就等于自变量在这点处的微分。
故答案为A。
解析
步骤 1：定义微分
微分是函数在某一点处的线性近似，对于函数$f(x)$，其在$x$点的微分定义为$df=f'(x)dx$，其中$f'(x)$是$f(x)$在$x$点的导数，$dx$是自变量$x$的改变量。
步骤 2：分析自变量的改变量
自变量$x$在某一点处的改变量记为$\Delta x$，它表示$x$从一个值变化到另一个值的差值。
步骤 3：比较改变量与微分
根据微分的定义，当$f(x)$是自变量$x$本身时，即$f(x)=x$，则$f'(x)=1$，因此$x$的微分$dx=1*\Delta x=\Delta x$。这表明，对于自变量$x$，其在一点处的改变量$\Delta x$就等于其在这点处的微分$dx$。
微分是函数在某一点处的线性近似，对于函数$f(x)$，其在$x$点的微分定义为$df=f'(x)dx$，其中$f'(x)$是$f(x)$在$x$点的导数，$dx$是自变量$x$的改变量。
步骤 2：分析自变量的改变量
自变量$x$在某一点处的改变量记为$\Delta x$，它表示$x$从一个值变化到另一个值的差值。
步骤 3：比较改变量与微分
根据微分的定义，当$f(x)$是自变量$x$本身时，即$f(x)=x$，则$f'(x)=1$，因此$x$的微分$dx=1*\Delta x=\Delta x$。这表明，对于自变量$x$，其在一点处的改变量$\Delta x$就等于其在这点处的微分$dx$。