用作图法说明下列各命题成立:(1)cup B=(A-AB)cup B,且右边两事件互斥;(2)cup B=(A-AB)cup B,且右边三事件两两互斥。
用作图法说明下列各命题成立:
(1)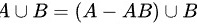 ,且右边两事件互斥;
,且右边两事件互斥;
(2)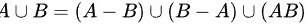 ,且右边三事件两两互斥。
,且右边三事件两两互斥。
题目解答
答案
1) 我们可以通过使用集合运算的性质来证明命题(1)。
首先,我们来证明 A∪B 包含于 (A-AB)∪B :
假设 x 属于 A∪B,那么 x 属于 A 或者 x 属于 B,或者同时属于 A 和 B。如果 x 属于 A 且不属于 AB,那么 x 属于 (A-AB)∪B。如果 x 属于 B 但不属于 A,则 x 仍然属于 (A-AB)∪B。如果 x 同时属于 A 和 B,那么 x 也属于 B,因此同样属于 (A-AB)∪B。因此,A∪B 包含于 (A-AB)∪B。
接下来,我们来证明 (A-AB)∪B 包含于 A∪B :
假设 y 属于 (A-AB)∪B,那么 y 属于 A-AB 或者 y 属于 B。如果 y 属于 A-AB,则 y 属于 A 且不属于 AB,因此 y 属于 A∪B。如果 y 属于 B,则 y 属于 A∪B。因此,(A-AB)∪B 包含于 A∪B。
由于 A∪B 包含于 (A-AB)∪B,并且 (A-AB)∪B 包含于 A∪B,因此 A∪B = (A-AB)∪B。
右边两事件互斥的证明:
(A-AB) 和 B 互斥,因为它们没有交集。即 (A-AB) ∩ B = ∅。
2) 同样地,我们可以通过使用集合运算的性质来证明命题(2)。
首先,我们来证明 A∪B 包含于 (A-B)∪(B-A)∪(AB) :
假设 x 属于 A∪B,那么 x 属于 A 或者 x 属于 B,或者同时属于 A 和 B。如果 x 属于 A 但不属于 B,那么 x 属于 (A-B)∪(B-A)∪(AB)。如果 x 属于 B 但不属于 A,则 x 同样属于 (A-B)∪(B-A)∪(AB)。如果 x 同时属于 A 和 B,那么 x 属于 AB,因此也属于 (A-B)∪(B-A)∪(AB)。因此,A∪B 包含于 (A-B)∪(B-A)∪(AB)。
接下来,我们来证明 (A-B)∪(B-A)∪(AB) 包含于 A∪B :
假设 y 属于 (A-B)∪(B-A)∪(AB),那么 y 属于 A-B 或者 y 属于 B-A 或者 y 属于 AB。如果 y 属于 A-B,则 y 属于 A 且不属于 B,因此 y 属于 A∪B。如果 y 属于 B-A,则 y 属于 B 且不属于 A,因此 y 属于 A∪B。如果 y 属于 AB,则 y 同时属于 A 和 B,因此 y 属于 A∪B。因此,(A-B)∪(B-A)∪(AB) 包含于 A∪B。
由于 A∪B 包含于 (A-B)∪(B-A)∪(AB),并且 (A-B)∪(B-A)∪(AB) 包含于 A∪B,因此 A∪B = (A-B)∪(B-A)∪(AB)。
右边三事件两两互斥的证明:
(A-B) 和 (B-A) 互斥,因为它们没有交集。即 (A-B) ∩ (B-A) = ∅。
(A-B) 和 AB 互斥,因为它们没有交集。即 (A-B) ∩ AB = ∅。
(B-A) 和 AB 互斥,因为它们没有交集。即 (B-A) ∩ AB = ∅。
最终答案:通过使用集合运算的性质,我们证明了命题(1)和(2)成立,并且给出了右边事件互斥的证明。