设f"(a)存在, '(a)neq 0 ,则 lim _(xarrow a)[ dfrac (1)(f'(a)(x-a))-dfrac (1)(f(x)-f(a))] = __
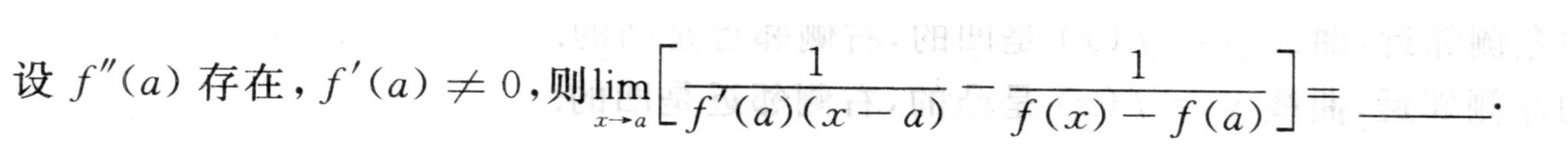
题目解答
答案
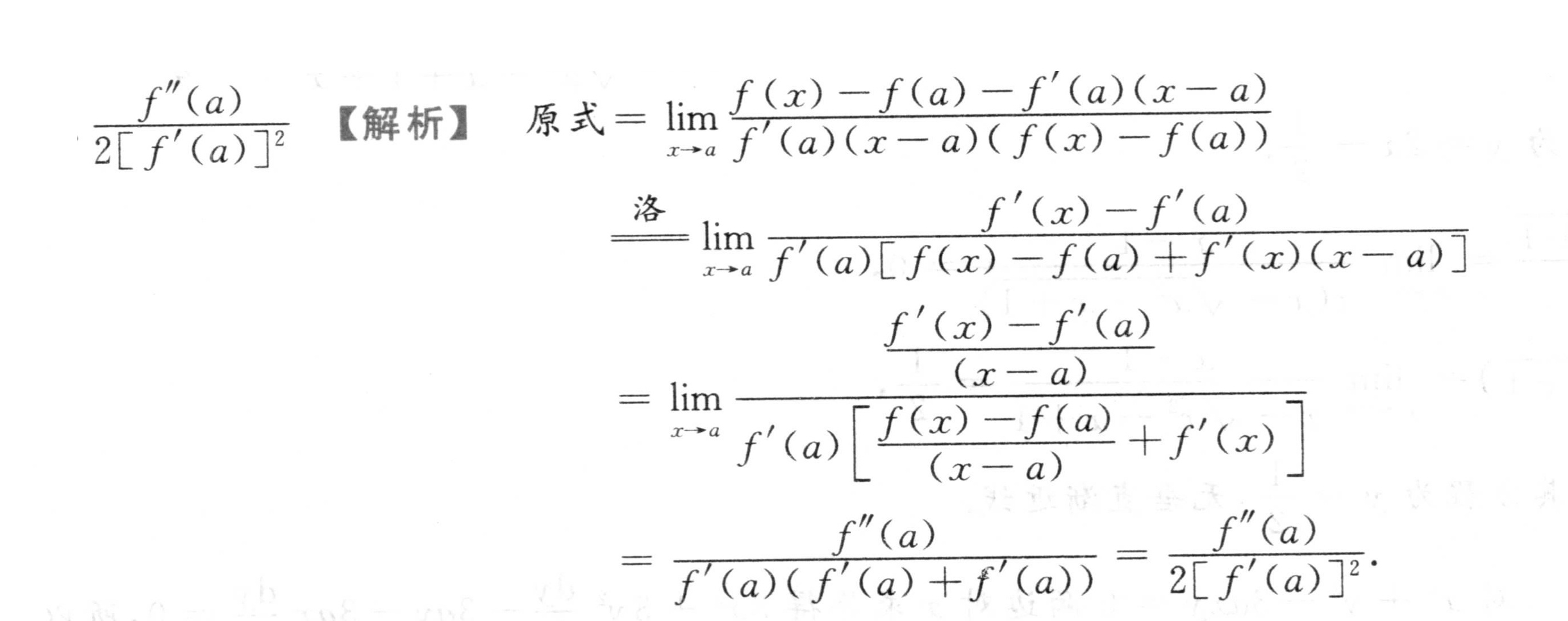
解析
考查要点:本题主要考查极限的计算,涉及导数的定义、泰勒展开或洛必达法则的应用,以及二阶导数的运用。
解题核心思路:
- 通分处理:将原式中的两个分式合并为一个分式,转化为分子分母的极限形式。
- 观察不定型:分子和分母在$x \to a$时均趋近于0,属于$\frac{0}{0}$型不定式,可考虑洛必达法则或泰勒展开。
- 关键步骤:通过两次求导(洛必达法则)或展开到二阶泰勒多项式,提取二阶导数$f''(a)$的信息,最终化简得到结果。
破题关键点:
- 识别分子中的二阶小量:分子$f(x)-f(a)-f'(a)(x-a)$对应泰勒展开的二阶余项,其主要部分为$\frac{1}{2}f''(a)(x-a)^2$。
- 分母的简化:利用$f(x)-f(a) \approx f'(a)(x-a)$近似分母,保留主部后化简。
步骤1:通分合并分式
原式可变形为:
$\begin{aligned}\lim _{x\rightarrow a}\left[ \dfrac {1}{f'(a)(x-a)}-\dfrac {1}{f(x)-f(a)} \right] &= \lim _{x\rightarrow a} \dfrac{f(x)-f(a) - f'(a)(x-a)}{f'(a)(x-a)(f(x)-f(a))}.\end{aligned}$
步骤2:应用泰勒展开
将$f(x)$在$a$处展开到二阶:
$f(x) = f(a) + f'(a)(x-a) + \dfrac{1}{2}f''(a)(x-a)^2 + o((x-a)^2).$
代入分子:
$f(x)-f(a) - f'(a)(x-a) = \dfrac{1}{2}f''(a)(x-a)^2 + o((x-a)^2).$
分母近似为:
$f'(a)(x-a)\left[f'(a)(x-a) + \dfrac{1}{2}f''(a)(x-a)^2\right] \approx f'(a)^2(x-a)^2.$
因此,极限化简为:
$\lim _{x\rightarrow a} \dfrac{\dfrac{1}{2}f''(a)(x-a)^2}{f'(a)^2(x-a)^2} = \dfrac{f''(a)}{2f'(a)^2}.$
步骤3(替代方法):洛必达法则
分子和分母均为$\frac{0}{0}$型,第一次求导:
- 分子导数:$f'(x) - f'(a)$
- 分母导数:$f'(a)\left[f(x)-f(a) + (x-a)f'(x)\right]$
再次应用洛必达法则(仍为$\frac{0}{0}$型):
- 分子二阶导数:$f''(x)$
- 分母二阶导数:$f'(a)\left[2f'(x) + (x-a)f''(x)\right]$
代入$x=a$,得极限值:
$\dfrac{f''(a)}{2f'(a)^2}.$