题目
已知二次型-|||-((x)_(1),(x)_(2),(x)_(3))=2({x)_(1)}^2+3({x)_(2)}^2+3({x)_(3)}^2+2a(x)_(2)(x)_(3)(agt 0),-|||-通过正交变换化为标准形 =({y)_(1)}^2+2({y)_(2)}^2+5({y)_(3)}^2, 求参数a及所用的正交变换矩阵.
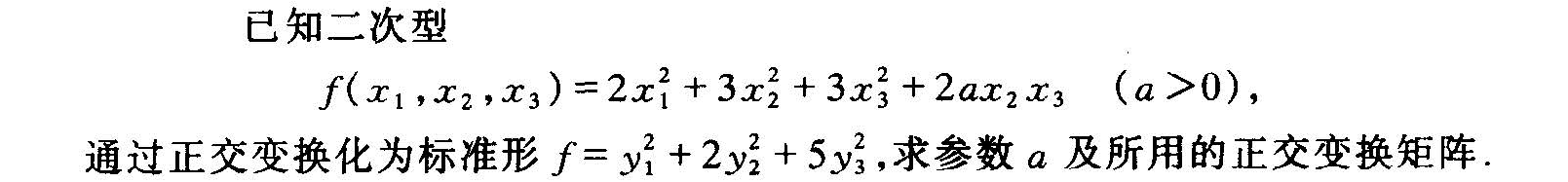
题目解答
答案

解析
步骤 1:确定二次型的矩阵表示
二次型 $f({x}_{1},{x}_{2},{x}_{3})=2{x}_{1}^{2}+3{{x}_{2}}^{2}+3{{x}_{3}}^{2}+2a{x}_{2}{x}_{3}$ 可以表示为矩阵形式 $f = \mathbf{x}^T A \mathbf{x}$,其中 $\mathbf{x} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}$,$A = \begin{pmatrix} 2 & 0 & 0 \\ 0 & 3 & a \\ 0 & a & 3 \end{pmatrix}$。
步骤 2:求矩阵A的特征值
矩阵A的特征值是方程 $\det(A - \lambda I) = 0$ 的解,其中 $I$ 是单位矩阵。计算得:
$$
\det(A - \lambda I) = \det \begin{pmatrix} 2-\lambda & 0 & 0 \\ 0 & 3-\lambda & a \\ 0 & a & 3-\lambda \end{pmatrix} = (2-\lambda)((3-\lambda)^2 - a^2) = 0
$$
解得特征值 $\lambda_1 = 2$,$\lambda_2 = 3 - a$,$\lambda_3 = 3 + a$。
步骤 3:根据标准形确定特征值
已知二次型的标准形为 $f={{y}_{1}}^{2}+2{{y}_{2}}^{2}+5{{y}_{3}}^{2}$,因此特征值为1, 2, 5。对比步骤2中的特征值,可以确定 $a = 2$。
步骤 4:求特征向量并正交化
对于特征值 $\lambda_1 = 2$,解方程 $(A - 2I)\mathbf{x} = 0$ 得到特征向量 $\mathbf{v}_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$。
对于特征值 $\lambda_2 = 1$,解方程 $(A - I)\mathbf{x} = 0$ 得到特征向量 $\mathbf{v}_2 = \begin{pmatrix} 0 \\ 1 \\ -1 \end{pmatrix}$。
对于特征值 $\lambda_3 = 5$,解方程 $(A - 5I)\mathbf{x} = 0$ 得到特征向量 $\mathbf{v}_3 = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}$。
将特征向量正交化并单位化,得到正交矩阵 $T = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 0 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}$。
二次型 $f({x}_{1},{x}_{2},{x}_{3})=2{x}_{1}^{2}+3{{x}_{2}}^{2}+3{{x}_{3}}^{2}+2a{x}_{2}{x}_{3}$ 可以表示为矩阵形式 $f = \mathbf{x}^T A \mathbf{x}$,其中 $\mathbf{x} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}$,$A = \begin{pmatrix} 2 & 0 & 0 \\ 0 & 3 & a \\ 0 & a & 3 \end{pmatrix}$。
步骤 2:求矩阵A的特征值
矩阵A的特征值是方程 $\det(A - \lambda I) = 0$ 的解,其中 $I$ 是单位矩阵。计算得:
$$
\det(A - \lambda I) = \det \begin{pmatrix} 2-\lambda & 0 & 0 \\ 0 & 3-\lambda & a \\ 0 & a & 3-\lambda \end{pmatrix} = (2-\lambda)((3-\lambda)^2 - a^2) = 0
$$
解得特征值 $\lambda_1 = 2$,$\lambda_2 = 3 - a$,$\lambda_3 = 3 + a$。
步骤 3:根据标准形确定特征值
已知二次型的标准形为 $f={{y}_{1}}^{2}+2{{y}_{2}}^{2}+5{{y}_{3}}^{2}$,因此特征值为1, 2, 5。对比步骤2中的特征值,可以确定 $a = 2$。
步骤 4:求特征向量并正交化
对于特征值 $\lambda_1 = 2$,解方程 $(A - 2I)\mathbf{x} = 0$ 得到特征向量 $\mathbf{v}_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$。
对于特征值 $\lambda_2 = 1$,解方程 $(A - I)\mathbf{x} = 0$ 得到特征向量 $\mathbf{v}_2 = \begin{pmatrix} 0 \\ 1 \\ -1 \end{pmatrix}$。
对于特征值 $\lambda_3 = 5$,解方程 $(A - 5I)\mathbf{x} = 0$ 得到特征向量 $\mathbf{v}_3 = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}$。
将特征向量正交化并单位化,得到正交矩阵 $T = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 0 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}$。