题目
求下列微分方程的通解或特解: ) (1+ex)yy'=(e)^x y(|)_(x=0)=0 .
求下列微分方程的通解或特解:
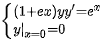
题目解答
答案
解:
分离变量:
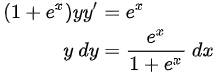
两边积分:
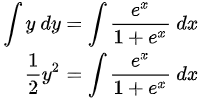
令 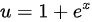 ,则
,则 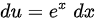
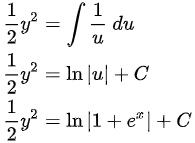
因为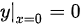 ,所以:
,所以:
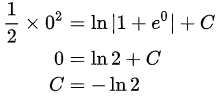
所以方程的解为:
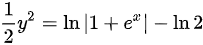
即
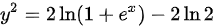
解析
步骤 1:分离变量
给定的微分方程是 $(1+ex)yy'={e}^{x}$。首先,我们分离变量,将 $y$ 和 $y'$ 放在方程的一边,将 $x$ 放在另一边。这可以写成 $yy'=\frac{{e}^{x}}{1+ex}$。
步骤 2:两边积分
对分离变量后的方程两边积分。左边是关于 $y$ 的积分,右边是关于 $x$ 的积分。即 $\int yy'dy=\int \frac{{e}^{x}}{1+ex}dx$。
步骤 3:求解积分
左边的积分是 $\frac{1}{2}y^2$,因为 $yy'$ 是 $y^2$ 的导数的一半。右边的积分需要使用代换法。令 $u=1+ex$,则 $du=edx$。因此,积分变为 $\int \frac{1}{u}du$,其结果是 $\ln|u|+C$。将 $u$ 替换回 $1+ex$,得到 $\ln|1+ex|+C$。
步骤 4:应用初始条件
给定 $y{|}_{x=0}=0$,代入得到 $\frac{1}{2}y^2{|}_{x=0}=\ln|1+e\cdot0|+C$,即 $0=\ln1+C$,从而 $C=0$。
步骤 5:写出方程的解
将 $C=0$ 代入,得到 $\frac{1}{2}y^2=\ln|1+ex|$。因为 $y{|}_{x=0}=0$,所以 $y$ 的值为 $0$ 时,$x$ 的值为 $0$,这表明 $y$ 的值为 $0$ 时,$1+ex$ 的值为 $1$,因此可以去掉绝对值符号。最终方程的解为 $\frac{1}{2}y^2=\ln(1+ex)$。
给定的微分方程是 $(1+ex)yy'={e}^{x}$。首先,我们分离变量,将 $y$ 和 $y'$ 放在方程的一边,将 $x$ 放在另一边。这可以写成 $yy'=\frac{{e}^{x}}{1+ex}$。
步骤 2:两边积分
对分离变量后的方程两边积分。左边是关于 $y$ 的积分,右边是关于 $x$ 的积分。即 $\int yy'dy=\int \frac{{e}^{x}}{1+ex}dx$。
步骤 3:求解积分
左边的积分是 $\frac{1}{2}y^2$,因为 $yy'$ 是 $y^2$ 的导数的一半。右边的积分需要使用代换法。令 $u=1+ex$,则 $du=edx$。因此,积分变为 $\int \frac{1}{u}du$,其结果是 $\ln|u|+C$。将 $u$ 替换回 $1+ex$,得到 $\ln|1+ex|+C$。
步骤 4:应用初始条件
给定 $y{|}_{x=0}=0$,代入得到 $\frac{1}{2}y^2{|}_{x=0}=\ln|1+e\cdot0|+C$,即 $0=\ln1+C$,从而 $C=0$。
步骤 5:写出方程的解
将 $C=0$ 代入,得到 $\frac{1}{2}y^2=\ln|1+ex|$。因为 $y{|}_{x=0}=0$,所以 $y$ 的值为 $0$ 时,$x$ 的值为 $0$,这表明 $y$ 的值为 $0$ 时,$1+ex$ 的值为 $1$,因此可以去掉绝对值符号。最终方程的解为 $\frac{1}{2}y^2=\ln(1+ex)$。