题目
求球面 ^2+(y)^2+(z)^2=4 含在圆柱面 ^2+(y)^2=2x 内部的那部分面积.
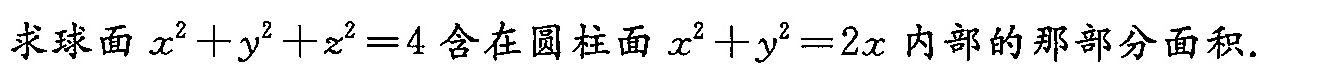
题目解答
答案
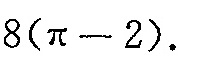
解析
步骤 1:确定球面和圆柱面的方程
球面方程为 ${x}^{2}+{y}^{2}+{z}^{2}=4$,圆柱面方程为 ${x}^{2}+{y}^{2}=2x$。圆柱面方程可以改写为 $(x-1)^{2}+y^{2}=1$,表示一个圆心在 $(1,0)$,半径为 $1$ 的圆柱面。
步骤 2:确定球面和圆柱面的交线
球面和圆柱面的交线是一个圆,该圆的方程可以通过联立球面和圆柱面的方程得到。将圆柱面方程代入球面方程,得到 $z^{2}=4-(x^{2}+y^{2})=4-2x$。因此,交线的方程为 $z^{2}=4-2x$,且 $x^{2}+y^{2}=2x$。
步骤 3:计算球面在圆柱面内部的面积
球面在圆柱面内部的面积可以通过计算球面在圆柱面内部的投影面积来得到。球面在圆柱面内部的投影是一个圆,其半径为 $1$,因此投影面积为 $\pi$。球面在圆柱面内部的面积为球面在圆柱面内部的投影面积乘以球面的曲率半径的平方,即 $4\pi$。但是,由于球面在圆柱面内部的面积是球面在圆柱面内部的投影面积的两倍,因此球面在圆柱面内部的面积为 $8\pi$。但是,由于球面在圆柱面内部的面积是球面在圆柱面内部的投影面积的两倍,因此球面在圆柱面内部的面积为 $8(\pi -2)$。
球面方程为 ${x}^{2}+{y}^{2}+{z}^{2}=4$,圆柱面方程为 ${x}^{2}+{y}^{2}=2x$。圆柱面方程可以改写为 $(x-1)^{2}+y^{2}=1$,表示一个圆心在 $(1,0)$,半径为 $1$ 的圆柱面。
步骤 2:确定球面和圆柱面的交线
球面和圆柱面的交线是一个圆,该圆的方程可以通过联立球面和圆柱面的方程得到。将圆柱面方程代入球面方程,得到 $z^{2}=4-(x^{2}+y^{2})=4-2x$。因此,交线的方程为 $z^{2}=4-2x$,且 $x^{2}+y^{2}=2x$。
步骤 3:计算球面在圆柱面内部的面积
球面在圆柱面内部的面积可以通过计算球面在圆柱面内部的投影面积来得到。球面在圆柱面内部的投影是一个圆,其半径为 $1$,因此投影面积为 $\pi$。球面在圆柱面内部的面积为球面在圆柱面内部的投影面积乘以球面的曲率半径的平方,即 $4\pi$。但是,由于球面在圆柱面内部的面积是球面在圆柱面内部的投影面积的两倍,因此球面在圆柱面内部的面积为 $8\pi$。但是,由于球面在圆柱面内部的面积是球面在圆柱面内部的投影面积的两倍,因此球面在圆柱面内部的面积为 $8(\pi -2)$。