题目
33 (1988,数一、二、三)若函数 y=f(x) 有 '((x)_(0))=dfrac (1)(2), 则当 Delta xarrow 0 时,该函数-|||-在 =(x)_(0) 处的微分dy是-|||-(A)与 Delta x 等价的无穷小. (B)与 Delta x 同阶的无穷小.-|||-(C)比 Delta x 低阶的无穷小. (D)比 Delta x 高阶的无穷小.
题目解答
答案
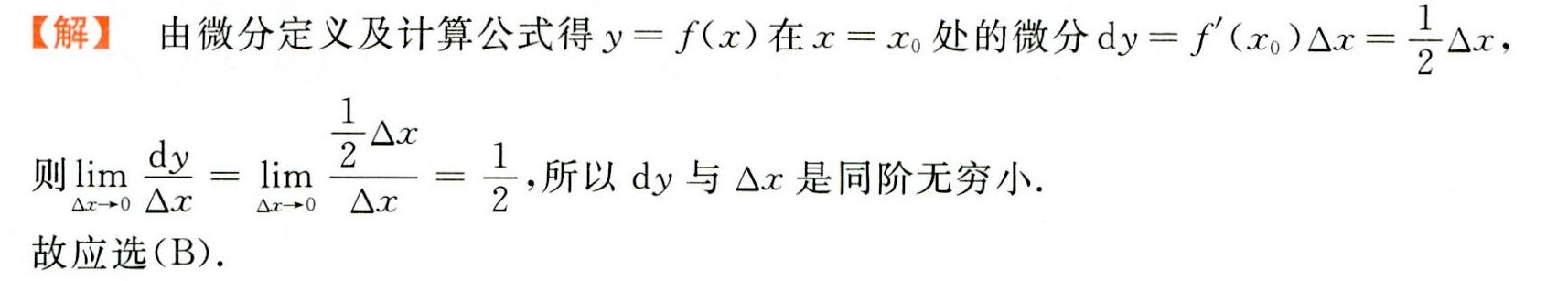
解析
步骤 1：微分定义
函数 $y=f(x)$ 在 $x=x_0$ 处的微分定义为 $dy=f'(x_0)\Delta x$，其中 $f'(x_0)$ 是函数在 $x=x_0$ 处的导数值，$\Delta x$ 是自变量的增量。
步骤 2：计算微分
根据题目条件，$f'(x_0)=\dfrac{1}{2}$，所以函数在 $x=x_0$ 处的微分 $dy=f'(x_0)\Delta x=\dfrac{1}{2}\Delta x$。
步骤 3：无穷小阶的比较
要判断 $dy$ 与 $\Delta x$ 的无穷小阶，需要计算 $\lim_{\Delta x\rightarrow 0}\dfrac{dy}{\Delta x}$。根据步骤 2 的结果，$\lim_{\Delta x\rightarrow 0}\dfrac{dy}{\Delta x}=\lim_{\Delta x\rightarrow 0}\dfrac{\dfrac{1}{2}\Delta x}{\Delta x}=\dfrac{1}{2}$。由于这个极限值为常数，说明 $dy$ 与 $\Delta x$ 是同阶无穷小。
函数 $y=f(x)$ 在 $x=x_0$ 处的微分定义为 $dy=f'(x_0)\Delta x$，其中 $f'(x_0)$ 是函数在 $x=x_0$ 处的导数值，$\Delta x$ 是自变量的增量。
步骤 2：计算微分
根据题目条件，$f'(x_0)=\dfrac{1}{2}$，所以函数在 $x=x_0$ 处的微分 $dy=f'(x_0)\Delta x=\dfrac{1}{2}\Delta x$。
步骤 3：无穷小阶的比较
要判断 $dy$ 与 $\Delta x$ 的无穷小阶，需要计算 $\lim_{\Delta x\rightarrow 0}\dfrac{dy}{\Delta x}$。根据步骤 2 的结果，$\lim_{\Delta x\rightarrow 0}\dfrac{dy}{\Delta x}=\lim_{\Delta x\rightarrow 0}\dfrac{\dfrac{1}{2}\Delta x}{\Delta x}=\dfrac{1}{2}$。由于这个极限值为常数，说明 $dy$ 与 $\Delta x$ 是同阶无穷小。