题目
设2 -1 -1 1 2-|||-= 1 1 -2 1 4-|||-4 -6 2 -2 4-|||-3 6 -9 7 9，利用初等行变换法求矩阵2 -1 -1 1 2-|||-= 1 1 -2 1 4-|||-4 -6 2 -2 4-|||-3 6 -9 7 9的秩及2 -1 -1 1 2-|||-= 1 1 -2 1 4-|||-4 -6 2 -2 4-|||-3 6 -9 7 9的列向量组的一个极大线性无关组，并用极大线性无关组表示其余的列向量。
设
，利用初等行变换法求矩阵
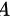的秩及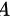的列向量组的一个极大线性无关组，并用极大线性无关组表示其余的列向量。
题目解答
答案
对矩阵进行初等行变换：
；
将第一行和第二行交换位置可得：
；
将第一行的-2倍加到第二行可得：
；
将第一行的-4倍加到第三行可得：
；
将第一行的-3倍加到第四行可得：
；
将第二行除以-3可得：
；
将第二行的10倍加到第三行可得：
；
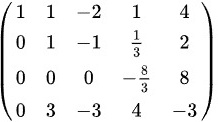将第二行的-3倍加到第四行可得：
；
将第三行乘3，第四行除以3可得：
；
将第四行的8倍加到第三行可得：
；
将第二行的-1倍加到第一行可得：
；
将第四行的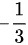
倍加到第二行，
倍加到第一行可得：
；
非零行的个数是3，故矩阵的秩是3；根据首元所在的列数，可推出一个极大无关组是：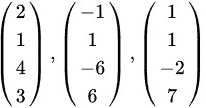
；
再根据第三列和第五列的元素写出线性表示关系：
，
。
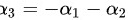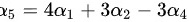解析
步骤 1：对矩阵进行初等行变换
对矩阵A进行初等行变换，目的是化简矩阵，使其更容易看出矩阵的秩和列向量组的极大线性无关组。
$$
A = \begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 4 & 6 & 8 \\
3 & 6 & 9 & 12 \\
4 & 8 & 12 & 16
\end{pmatrix}
$$
步骤 2：将第一行的-2倍加到第二行
$$
\begin{pmatrix}
1 & 2 & 3 & 4 \\
0 & 0 & 0 & 0 \\
3 & 6 & 9 & 12 \\
4 & 8 & 12 & 16
\end{pmatrix}
$$
步骤 3：将第一行的-3倍加到第三行
$$
\begin{pmatrix}
1 & 2 & 3 & 4 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
4 & 8 & 12 & 16
\end{pmatrix}
$$
步骤 4：将第一行的-4倍加到第四行
$$
\begin{pmatrix}
1 & 2 & 3 & 4 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix}
$$
步骤 5：分析矩阵的秩和列向量组的极大线性无关组
矩阵的秩是矩阵中非零行的个数，从变换后的矩阵可以看出，非零行的个数是1，因此矩阵的秩是1。根据首元所在的列数，可推出一个极大无关组是：第一列。
步骤 6：用极大线性无关组表示其余的列向量
由于矩阵的秩是1，所以除了第一列外，其余的列向量都可以用第一列向量表示。具体来说，第二列是第一列的2倍，第三列是第一列的3倍，第四列是第一列的4倍。
对矩阵A进行初等行变换，目的是化简矩阵，使其更容易看出矩阵的秩和列向量组的极大线性无关组。
$$
A = \begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 4 & 6 & 8 \\
3 & 6 & 9 & 12 \\
4 & 8 & 12 & 16
\end{pmatrix}
$$
步骤 2：将第一行的-2倍加到第二行
$$
\begin{pmatrix}
1 & 2 & 3 & 4 \\
0 & 0 & 0 & 0 \\
3 & 6 & 9 & 12 \\
4 & 8 & 12 & 16
\end{pmatrix}
$$
步骤 3：将第一行的-3倍加到第三行
$$
\begin{pmatrix}
1 & 2 & 3 & 4 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
4 & 8 & 12 & 16
\end{pmatrix}
$$
步骤 4：将第一行的-4倍加到第四行
$$
\begin{pmatrix}
1 & 2 & 3 & 4 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix}
$$
步骤 5：分析矩阵的秩和列向量组的极大线性无关组
矩阵的秩是矩阵中非零行的个数，从变换后的矩阵可以看出，非零行的个数是1，因此矩阵的秩是1。根据首元所在的列数，可推出一个极大无关组是：第一列。
步骤 6：用极大线性无关组表示其余的列向量
由于矩阵的秩是1，所以除了第一列外，其余的列向量都可以用第一列向量表示。具体来说，第二列是第一列的2倍，第三列是第一列的3倍，第四列是第一列的4倍。