题目
用布尔代数化简法化简该事故树求其最小割集;求该事故树的最小径集;画出以最小径集表示的事故树的等效图。T-|||-M1 M2-|||-+ 十-|||-M3 M4 X5 X6 X7-|||-±-|||-X1 x2 X3 X4
用布尔代数化简法化简该事故树求其最小割集;求该事故树的最小径集;画出以最小径集表示的事故树的等效图。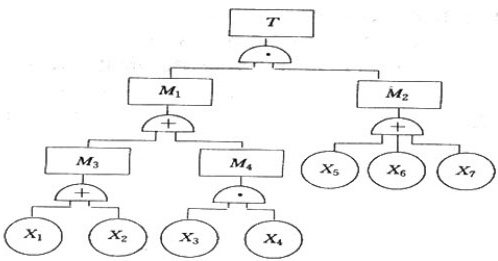

题目解答
答案
最佳答案
用布尔代数化简法求最小割集: T=M1M2=(M3+M4)(x5+x6+x7)=[(x1+x2)+x3x4](x5+x6+x7)=x1x5+x1x6+x1x7+x2x5+x2x6+x2x7+x3x4x5+x3x4x6+x3x4x7 得到9个最小割集,分别为: G1={x1,x5) G2={x1,x6) G3={x1,x7) G4={x2,x5} G5={x2,x6} G6={x2,x7) G7={x3,x4,x5} G8={x3,x4,x6) G9={x3,x4,x7) 用布尔代数化简法求最小径集: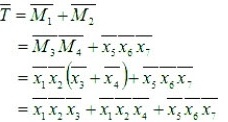 得到事故树的3割最小径集,分别为: P1={x1,x2,x3) p2={x1,x2,x4) P3={x5,x6,x7) 以最小径集表示的等效图为:
得到事故树的3割最小径集,分别为: P1={x1,x2,x3) p2={x1,x2,x4) P3={x5,x6,x7) 以最小径集表示的等效图为: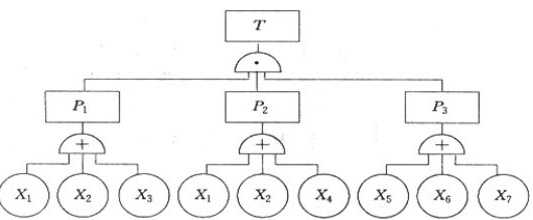
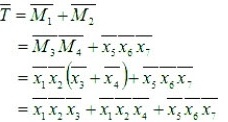 得到事故树的3割最小径集,分别为: P1={x1,x2,x3) p2={x1,x2,x4) P3={x5,x6,x7) 以最小径集表示的等效图为:
得到事故树的3割最小径集,分别为: P1={x1,x2,x3) p2={x1,x2,x4) P3={x5,x6,x7) 以最小径集表示的等效图为:
解析
步骤 1:化简最小割集
根据题目给出的事故树结构,我们首先需要化简最小割集。事故树的结构为:T = M1M2,其中M1 = M3 + M4,M2 = X5 + X6 + X7,M3 = X1 + X2,M4 = X3X4。将这些关系代入,得到:
T = (M3 + M4)(X5 + X6 + X7) = [(X1 + X2) + X3X4](X5 + X6 + X7)
步骤 2:化简最小径集
接下来,我们化简最小径集。首先,我们求出T的补集,即$\overline{T}$。根据德摩根定律,我们有:
$\overline{T} = \overline{M1} + \overline{M2} = \overline{M3M4} + \overline{X5X6X7} = \overline{M3} + \overline{M4} + \overline{X5} + \overline{X6} + \overline{X7}$
代入M3和M4的表达式,得到:
$\overline{T} = \overline{X1 + X2} + \overline{X3X4} + \overline{X5} + \overline{X6} + \overline{X7} = \overline{X1}\overline{X2} + \overline{X3} + \overline{X4} + \overline{X5} + \overline{X6} + \overline{X7}$
步骤 3:求最小割集和最小径集
根据步骤1和步骤2的化简结果,我们可以得到最小割集和最小径集。最小割集为:
G1 = {X1, X5}, G2 = {X1, X6}, G3 = {X1, X7}, G4 = {X2, X5}, G5 = {X2, X6}, G6 = {X2, X7}, G7 = {X3, X4, X5}, G8 = {X3, X4, X6}, G9 = {X3, X4, X7}
最小径集为:
P1 = {X1, X2, X3}, P2 = {X1, X2, X4}, P3 = {X5, X6, X7}
步骤 4:画出以最小径集表示的事故树的等效图
根据最小径集,我们可以画出以最小径集表示的事故树的等效图。等效图如下所示:
T P1 P2 P3 + + + X1 X2 X3 x1 x2 x4 X5 X6 x7
根据题目给出的事故树结构,我们首先需要化简最小割集。事故树的结构为:T = M1M2,其中M1 = M3 + M4,M2 = X5 + X6 + X7,M3 = X1 + X2,M4 = X3X4。将这些关系代入,得到:
T = (M3 + M4)(X5 + X6 + X7) = [(X1 + X2) + X3X4](X5 + X6 + X7)
步骤 2:化简最小径集
接下来,我们化简最小径集。首先,我们求出T的补集,即$\overline{T}$。根据德摩根定律,我们有:
$\overline{T} = \overline{M1} + \overline{M2} = \overline{M3M4} + \overline{X5X6X7} = \overline{M3} + \overline{M4} + \overline{X5} + \overline{X6} + \overline{X7}$
代入M3和M4的表达式,得到:
$\overline{T} = \overline{X1 + X2} + \overline{X3X4} + \overline{X5} + \overline{X6} + \overline{X7} = \overline{X1}\overline{X2} + \overline{X3} + \overline{X4} + \overline{X5} + \overline{X6} + \overline{X7}$
步骤 3:求最小割集和最小径集
根据步骤1和步骤2的化简结果,我们可以得到最小割集和最小径集。最小割集为:
G1 = {X1, X5}, G2 = {X1, X6}, G3 = {X1, X7}, G4 = {X2, X5}, G5 = {X2, X6}, G6 = {X2, X7}, G7 = {X3, X4, X5}, G8 = {X3, X4, X6}, G9 = {X3, X4, X7}
最小径集为:
P1 = {X1, X2, X3}, P2 = {X1, X2, X4}, P3 = {X5, X6, X7}
步骤 4:画出以最小径集表示的事故树的等效图
根据最小径集,我们可以画出以最小径集表示的事故树的等效图。等效图如下所示:
T P1 P2 P3 + + + X1 X2 X3 x1 x2 x4 X5 X6 x7