题目
因式分解:x^4-y^4.
因式分解:$$x^4-y^4$$.
题目解答
答案
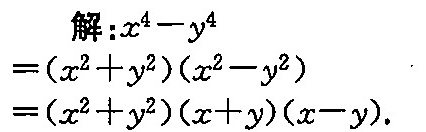
解析
步骤 1:识别公式
识别出给定的表达式是一个差平方的形式,即 ${x}^{4}-{y}^{4}$ 可以写成 ${x}^{2^2}-{y}^{2^2}$,这符合差平方的模式 ${a}^{2}-{b}^{2}$,其中 $a={x}^{2}$,$b={y}^{2}$。
步骤 2:应用差平方公式
应用差平方公式 ${a}^{2}-{b}^{2}=(a+b)(a-b)$,将 ${x}^{4}-{y}^{4}$ 写成 $({x}^{2}+{y}^{2})({x}^{2}-{y}^{2})$。
步骤 3:进一步分解
注意到 ${x}^{2}-{y}^{2}$ 也是差平方的形式,可以进一步分解为 $(x+y)(x-y)$。因此,整个表达式可以分解为 $({x}^{2}+{y}^{2})(x+y)(x-y)$。
识别出给定的表达式是一个差平方的形式,即 ${x}^{4}-{y}^{4}$ 可以写成 ${x}^{2^2}-{y}^{2^2}$,这符合差平方的模式 ${a}^{2}-{b}^{2}$,其中 $a={x}^{2}$,$b={y}^{2}$。
步骤 2:应用差平方公式
应用差平方公式 ${a}^{2}-{b}^{2}=(a+b)(a-b)$,将 ${x}^{4}-{y}^{4}$ 写成 $({x}^{2}+{y}^{2})({x}^{2}-{y}^{2})$。
步骤 3:进一步分解
注意到 ${x}^{2}-{y}^{2}$ 也是差平方的形式,可以进一步分解为 $(x+y)(x-y)$。因此,整个表达式可以分解为 $({x}^{2}+{y}^{2})(x+y)(x-y)$。