题目
曲线=dfrac (1)(x)+ln (1+(e)^x)-|||-__的渐近线的条数为( )A.0B.1C.2D.3.
曲线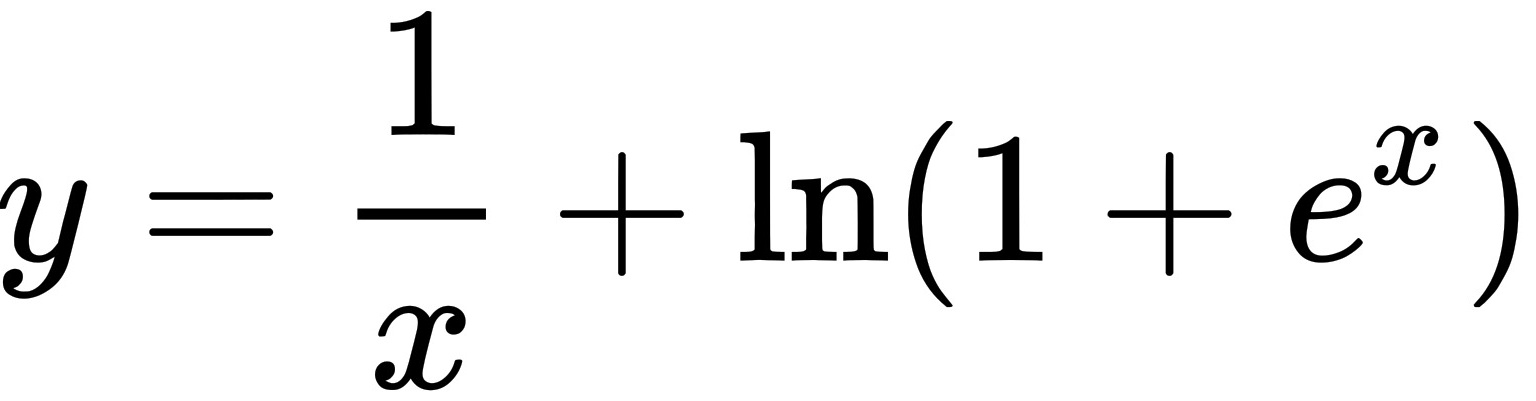 的渐近线的条数为( )
的渐近线的条数为( )
B.1
C.2
D.3
.
题目解答
答案
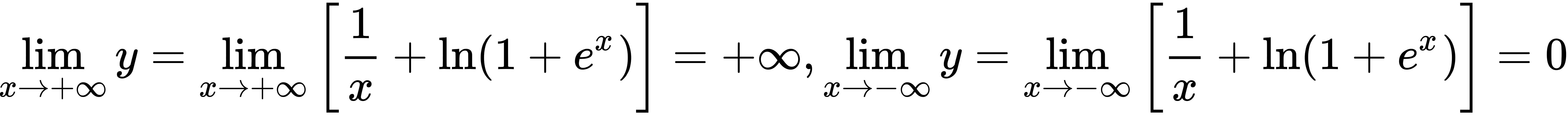 ,
,
所以y=0是曲线的水平渐近线;
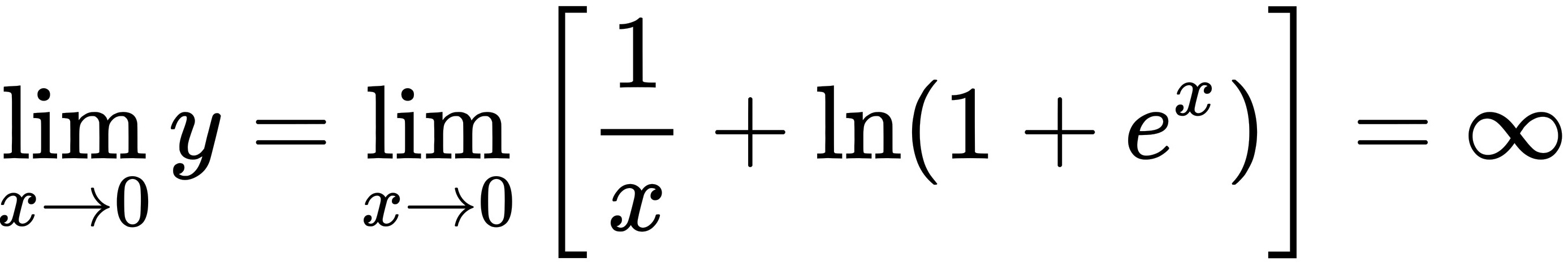 ,所以x=0是曲线的垂直渐近线;
,所以x=0是曲线的垂直渐近线;
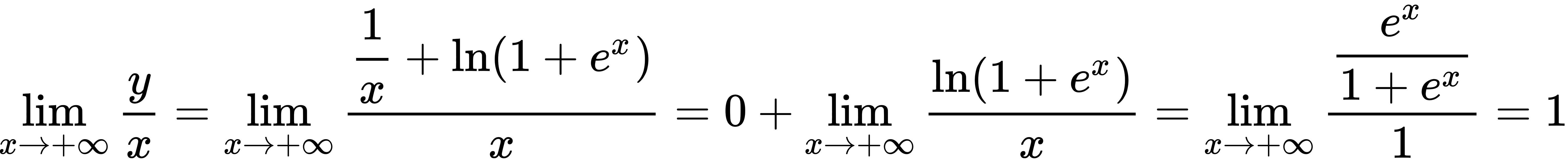
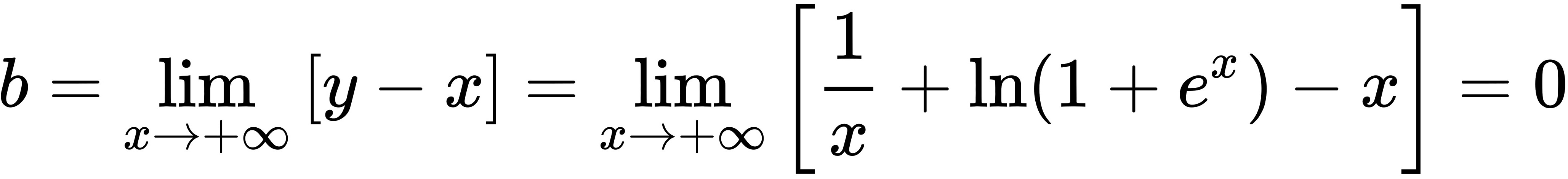 ,所以y=x是曲线的斜渐近线.
,所以y=x是曲线的斜渐近线.
共3条渐近线
故应选:D.
.解析
本题考查曲线渐近线的求解,涉及水平渐近线、垂直渐近线、斜渐近线的判断。解题核心思路是:
- 水平渐近线:计算当$x \rightarrow +\infty$和$x \rightarrow -\infty$时函数的极限;
- 垂直渐近线:寻找函数趋向于无穷大的点;
- 斜渐近线:当$x \rightarrow +\infty$或$x \rightarrow -\infty$时,若函数与某一次函数的差趋向于常数,则存在斜渐近线。
关键点在于正确处理自然对数与指数函数的组合形式,通过近似展开或变形简化极限计算。
1. 水平渐近线
-
当$x \rightarrow +\infty$时:
$\ln(1+e^x) = \ln(e^x(1+e^{-x})) = x + \ln(1+e^{-x}) \approx x + e^{-x}$
因此:
$y = \frac{1}{x} + \ln(1+e^x) \approx \frac{1}{x} + x + e^{-x} \rightarrow +\infty$
无水平渐近线。 -
当$x \rightarrow -\infty$时:
$e^x \rightarrow 0 \Rightarrow \ln(1+e^x) \approx e^x$
因此:
$y = \frac{1}{x} + e^x \rightarrow 0$
水平渐近线为$y=0$。
2. 垂直渐近线
- 当$x \rightarrow 0$时:
$\frac{1}{x} \rightarrow +\infty, \quad \ln(1+e^0) = \ln 2$
因此:
$y = \frac{1}{x} + \ln 2 \rightarrow +\infty$
垂直渐近线为$x=0$。
3. 斜渐近线
- 当$x \rightarrow +\infty$时:
$y \approx x + \frac{1}{x} + e^{-x}$
设斜渐近线为$y = ax + b$,则:
$a = \lim_{x \rightarrow +\infty} \frac{y}{x} = \lim_{x \rightarrow +\infty} \frac{x + \frac{1}{x} + e^{-x}}{x} = 1$
$b = \lim_{x \rightarrow +\infty} (y - ax) = \lim_{x \rightarrow +\infty} \left(\frac{1}{x} + e^{-x}\right) = 0$
斜渐近线为$y = x$。