题目
4.设X,Y是相互独立的随机变量,其概率密度分别为-|||-_(x)(x)= ) 1,0leqslant xleqslant 1 0, .-|||-求 =x+y 的概率密度.

题目解答
答案
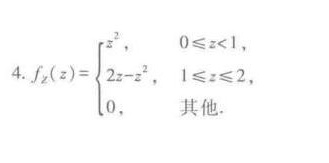
解析
考查要点:本题主要考查独立随机变量和的卷积公式的应用,需要根据X和Y的定义域分段讨论积分区间。
解题思路:
- 确定Z的可能取值范围:由于X和Y均在[0,1]上,故Z=X+Y的取值范围为[0,2]。
- 分段讨论积分区间:
- 当0 ≤ z < 1时,x的取值范围为[0, z];
- 当1 ≤ z ≤ 2时,x的取值范围为[z−1, 1]。
- 应用卷积公式:分别对两个区间进行积分,得到对应的概率密度表达式。
关键点:
- 独立性保证了联合密度为各自密度的乘积;
- 积分上下限需根据z的不同取值严格确定。
步骤1:确定Z的取值范围
X和Y均在[0,1]上,故Z = X + Y的取值范围为[0, 2]。
步骤2:分段讨论积分区间
-
当0 ≤ z < 1时:
- X的取值范围为[0, z](因为Y = z − x ≥ 0要求x ≤ z)。
- 积分区间为x ∈ [0, z]。
-
当1 ≤ z ≤ 2时:
- X的取值范围为[z − 1, 1](因为Y = z − x ≤ 1要求x ≥ z − 1)。
- 积分区间为x ∈ [z − 1, 1]。
步骤3:应用卷积公式计算
-
0 ≤ z < 1:
$f_Z(z) = \int_{0}^{z} f_X(x) f_Y(z - x) \, dx = \int_{0}^{z} 1 \cdot 2(z - x) \, dx = \left[ 2zx - x^2 \right]_{0}^{z} = z^2.$ -
1 ≤ z ≤ 2:
$f_Z(z) = \int_{z-1}^{1} 1 \cdot 2(z - x) \, dx = \left[ 2zx - x^2 \right]_{z-1}^{1} = (2z - 1) - \left[ 2z(z - 1) - (z - 1)^2 \right] = 2z - z^2.$
步骤4:综合结果
最终,Z的概率密度函数为:
$f_Z(z) =
\begin{cases}z^2, & 0 \leq z < 1, \\2z - z^2, & 1 \leq z \leq 2, \\0, & \text{其他}.\end{cases}$