题目
2、计算 =iint ((x)^2+(y)^2+2y)dxdy, 其中D是由圆 ^2+(y)^2=2x 围成的平面区域。
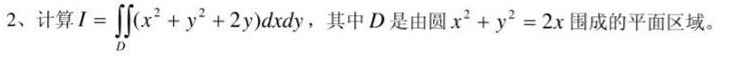
题目解答
答案

解析
步骤 1:确定积分区域
给定的圆方程为 ${x}^{2}+{y}^{2}=2x$,可以改写为 $(x-1)^2+y^2=1$,这是一个以 $(1,0)$ 为圆心,半径为 $1$ 的圆。因此,积分区域 $D$ 是这个圆内部的区域。
步骤 2:转换为极坐标
为了简化积分,我们使用极坐标变换。设 $x=r\cos\theta$,$y=r\sin\theta$,则 $x^2+y^2=r^2$。积分区域 $D$ 在极坐标系中表示为 $0\leq r\leq 2\cos\theta$,$-\frac{\pi}{2}\leq\theta\leq\frac{\pi}{2}$。
步骤 3:计算积分
将原积分转换为极坐标形式,得到
$$
I=\iint_D (r^2+2r\sin\theta)rdrd\theta = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_0^{2\cos\theta} (r^3+2r^2\sin\theta)drd\theta
$$
计算内层积分
$$
\int_0^{2\cos\theta} (r^3+2r^2\sin\theta)dr = \left[\frac{r^4}{4}+2\sin\theta\frac{r^3}{3}\right]_0^{2\cos\theta} = \frac{(2\cos\theta)^4}{4}+2\sin\theta\frac{(2\cos\theta)^3}{3}
$$
$$
= 4\cos^4\theta+\frac{16}{3}\sin\theta\cos^3\theta
$$
计算外层积分
$$
I = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(4\cos^4\theta+\frac{16}{3}\sin\theta\cos^3\theta\right)d\theta
$$
$$
= 4\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos^4\theta d\theta + \frac{16}{3}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin\theta\cos^3\theta d\theta
$$
注意到 $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin\theta\cos^3\theta d\theta = 0$,因为被积函数是奇函数,积分区间关于原点对称。因此,我们只需要计算第一项
$$
4\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos^4\theta d\theta = 4\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(\frac{1+\cos2\theta}{2}\right)^2 d\theta = 4\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(\frac{1}{4}+\frac{1}{2}\cos2\theta+\frac{1}{4}\cos^22\theta\right) d\theta
$$
$$
= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(1+2\cos2\theta+\cos^22\theta\right) d\theta = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(1+2\cos2\theta+\frac{1+\cos4\theta}{2}\right) d\theta
$$
$$
= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(\frac{3}{2}+2\cos2\theta+\frac{1}{2}\cos4\theta\right) d\theta = \frac{3}{2}\pi
$$
给定的圆方程为 ${x}^{2}+{y}^{2}=2x$,可以改写为 $(x-1)^2+y^2=1$,这是一个以 $(1,0)$ 为圆心,半径为 $1$ 的圆。因此,积分区域 $D$ 是这个圆内部的区域。
步骤 2:转换为极坐标
为了简化积分,我们使用极坐标变换。设 $x=r\cos\theta$,$y=r\sin\theta$,则 $x^2+y^2=r^2$。积分区域 $D$ 在极坐标系中表示为 $0\leq r\leq 2\cos\theta$,$-\frac{\pi}{2}\leq\theta\leq\frac{\pi}{2}$。
步骤 3:计算积分
将原积分转换为极坐标形式,得到
$$
I=\iint_D (r^2+2r\sin\theta)rdrd\theta = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_0^{2\cos\theta} (r^3+2r^2\sin\theta)drd\theta
$$
计算内层积分
$$
\int_0^{2\cos\theta} (r^3+2r^2\sin\theta)dr = \left[\frac{r^4}{4}+2\sin\theta\frac{r^3}{3}\right]_0^{2\cos\theta} = \frac{(2\cos\theta)^4}{4}+2\sin\theta\frac{(2\cos\theta)^3}{3}
$$
$$
= 4\cos^4\theta+\frac{16}{3}\sin\theta\cos^3\theta
$$
计算外层积分
$$
I = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(4\cos^4\theta+\frac{16}{3}\sin\theta\cos^3\theta\right)d\theta
$$
$$
= 4\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos^4\theta d\theta + \frac{16}{3}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin\theta\cos^3\theta d\theta
$$
注意到 $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin\theta\cos^3\theta d\theta = 0$,因为被积函数是奇函数,积分区间关于原点对称。因此,我们只需要计算第一项
$$
4\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos^4\theta d\theta = 4\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(\frac{1+\cos2\theta}{2}\right)^2 d\theta = 4\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(\frac{1}{4}+\frac{1}{2}\cos2\theta+\frac{1}{4}\cos^22\theta\right) d\theta
$$
$$
= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(1+2\cos2\theta+\cos^22\theta\right) d\theta = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(1+2\cos2\theta+\frac{1+\cos4\theta}{2}\right) d\theta
$$
$$
= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \left(\frac{3}{2}+2\cos2\theta+\frac{1}{2}\cos4\theta\right) d\theta = \frac{3}{2}\pi
$$