题目
当时,与为等价无穷小,则( ) ABCD
当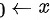 时,
时,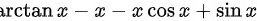 与
与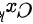 为等价无穷小,则( )
为等价无穷小,则( )
A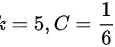
B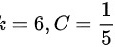
C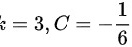
D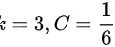
题目解答
答案
由于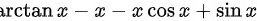
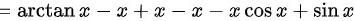
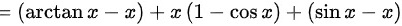
由于当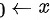 时,由等价无穷小可得:
时,由等价无穷小可得:
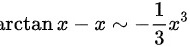 ,
,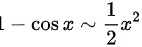 ,
,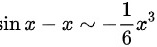
则当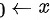 时,
时,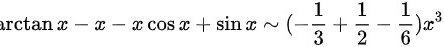
由于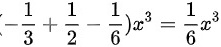 ,则
,则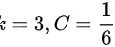 ,故答案为D。
,故答案为D。
解析
步骤 1:分析等价无穷小
当)←x时,$\arctan x-x-x\cos x+\sin x$与$x^o$为等价无穷小,意味着它们的比值在x趋于0时的极限为1。因此,我们需要找到$\arctan x-x-x\cos x+\sin x$的等价无穷小形式。
步骤 2:利用等价无穷小替换
我们知道当x趋于0时,$\arctan x \sim x - \dfrac{1}{3}x^3$,$1-\cos x \sim \dfrac{1}{2}x^2$,$\sin x \sim x - \dfrac{1}{6}x^3$。因此,我们可以将$\arctan x-x-x\cos x+\sin x$中的每一项用其等价无穷小替换。
步骤 3:计算等价无穷小
将$\arctan x-x-x\cos x+\sin x$中的每一项用其等价无穷小替换,得到:
$\arctan x-x-x\cos x+\sin x \sim (x - \dfrac{1}{3}x^3) - x - x(1 - \dfrac{1}{2}x^2) + (x - \dfrac{1}{6}x^3)$
$= -\dfrac{1}{3}x^3 - x + \dfrac{1}{2}x^3 - \dfrac{1}{6}x^3$
$= (-\dfrac{1}{3} + \dfrac{1}{2} - \dfrac{1}{6})x^3$
$= \dfrac{1}{6}x^3$
步骤 4:确定等价无穷小的系数
由于$\arctan x-x-x\cos x+\sin x$与$x^o$为等价无穷小,因此$x^o$的系数应该与$\dfrac{1}{6}x^3$的系数相同。因此,$o=3$,$C=\dfrac{1}{6}$。
当)←x时,$\arctan x-x-x\cos x+\sin x$与$x^o$为等价无穷小,意味着它们的比值在x趋于0时的极限为1。因此,我们需要找到$\arctan x-x-x\cos x+\sin x$的等价无穷小形式。
步骤 2:利用等价无穷小替换
我们知道当x趋于0时,$\arctan x \sim x - \dfrac{1}{3}x^3$,$1-\cos x \sim \dfrac{1}{2}x^2$,$\sin x \sim x - \dfrac{1}{6}x^3$。因此,我们可以将$\arctan x-x-x\cos x+\sin x$中的每一项用其等价无穷小替换。
步骤 3:计算等价无穷小
将$\arctan x-x-x\cos x+\sin x$中的每一项用其等价无穷小替换,得到:
$\arctan x-x-x\cos x+\sin x \sim (x - \dfrac{1}{3}x^3) - x - x(1 - \dfrac{1}{2}x^2) + (x - \dfrac{1}{6}x^3)$
$= -\dfrac{1}{3}x^3 - x + \dfrac{1}{2}x^3 - \dfrac{1}{6}x^3$
$= (-\dfrac{1}{3} + \dfrac{1}{2} - \dfrac{1}{6})x^3$
$= \dfrac{1}{6}x^3$
步骤 4:确定等价无穷小的系数
由于$\arctan x-x-x\cos x+\sin x$与$x^o$为等价无穷小,因此$x^o$的系数应该与$\dfrac{1}{6}x^3$的系数相同。因此,$o=3$,$C=\dfrac{1}{6}$。