题目
2.计算下列行列式.-|||--ab ac ae-|||-(3) bd -cd de-|||-bf cf -ef

题目解答
答案
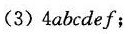
解析
考查要点:本题主要考查行列式的计算,特别是通过提取行公因子简化行列式的技巧,以及对3×3行列式的展开方法。
解题核心思路:
- 观察行列式结构,发现每行存在公因子,提取后可大幅简化计算。
- 提取公因子:第一行提取$a$,第二行提取$d$,第三行提取$f$,行列式变为$adf$乘以剩余部分的行列式。
- 计算剩余行列式:通过展开法或行变换进一步简化,最终得到结果。
破题关键点:
- 识别行公因子是简化计算的关键,避免直接展开原行列式的繁琐计算。
- 正确展开简化后的行列式,注意符号和余子式的计算。
步骤1:提取行公因子
原行列式为:
$\begin{vmatrix}-ab & ac & ae \\bd & -cd & de \\bf & cf & -ef\end{vmatrix}$
- 第一行:提取公因子$a$,剩余元素为$(-b, c, e)$。
- 第二行:提取公因子$d$,剩余元素为$(b, -c, e)$。
- 第三行:提取公因子$f$,剩余元素为$(b, c, -e)$。
提取后行列式变为:
$adf \cdot \begin{vmatrix}-b & c & e \\b & -c & e \\b & c & -e\end{vmatrix}$
步骤2:计算剩余行列式
设剩余行列式为:
$D = \begin{vmatrix}-b & c & e \\b & -c & e \\b & c & -e\end{vmatrix}$
按第一行展开:
$D = -b \cdot \begin{vmatrix}-c & e \\ c & -e\end{vmatrix} - c \cdot \begin{vmatrix}b & e \\ b & -e\end{vmatrix} + e \cdot \begin{vmatrix}b & -c \\ b & c\end{vmatrix}$
逐项计算:
- 第一项:
$\begin{vmatrix}-c & e \\ c & -e\end{vmatrix} = (-c)(-e) - e \cdot c = ce - ce = 0$ - 第二项:
$\begin{vmatrix}b & e \\ b & -e\end{vmatrix} = b(-e) - e \cdot b = -be - be = -2be$ - 第三项:
$\begin{vmatrix}b & -c \\ b & c\end{vmatrix} = b \cdot c - (-c) \cdot b = bc + bc = 2bc$
代入展开式:
$D = -b \cdot 0 - c \cdot (-2be) + e \cdot 2bc = 0 + 2bce + 2bce = 4bce$
步骤3:合并结果
原行列式最终结果为:
$adf \cdot 4bce = 4abcdef$