题目
袋中有 a 只白球, b 只红球, k 个人 依次在袋中取一只球, 在不 放回抽样下, 求第 2 个人取到白球的概率____________ .
袋中有 a 只白球, b 只红球, k 个人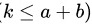 
依次在袋中取一只球, 在不 放回抽样下, 求第 2 个人取到白球的概率____________ .
题目解答
答案
题目要求求出第 2 个人取到白球的概率。
设事件 A 表示第 2 个人取到白球，事件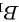
表示第 1 个人取到白球，事件 
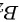表示第 1 个人取到红球。则根据全概率公式，我们有：
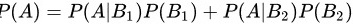
由于袋中有 a 只白球，b 只红球，所以：
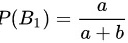
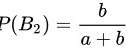
当第 1 个人取到白球时，袋中还剩下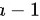
只白球和 b 只红球，所以：
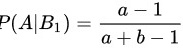
当第 1 个人取到红球时，袋中还剩下 a 只白球和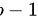 
只红球，所以：
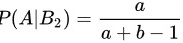
将上述结果代入全概率公式中，得：
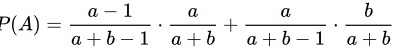
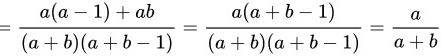
所以，第 2 个人取到白球的概率为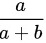
。
解析
步骤 1：定义事件
设事件 A 表示第 2 个人取到白球，事件B1 表示第 1 个人取到白球，事件B2 表示第 1 个人取到红球。
步骤 2：应用全概率公式
根据全概率公式，我们有：
$P(A)=P(A|{B}_{1})P({B}_{1})+P(A|{B}_{2})P({B}_{2})$
步骤 3：计算条件概率
由于袋中有 a 只白球，b 只红球，所以：
$P({B}_{1})=\dfrac {a}{a+b}$
$P({B}_{2})=\dfrac {b}{a+b}$
当第 1 个人取到白球时，袋中还剩下 a-1 只白球和 b 只红球，所以：
$P(A|{B}_{1})=\dfrac {a-1}{a+b-1}$
当第 1 个人取到红球时，袋中还剩下 a 只白球和 b-1 只红球，所以：
$P(A|{B}_{2})=\dfrac {a}{a+b-1}$
步骤 4：代入全概率公式
将上述结果代入全概率公式中，得：
$P(A)=\dfrac {a-1}{a+b-1}\cdot \dfrac {a}{a+b}+\dfrac {a}{a+b-1}\cdot \dfrac {b}{a+b}$
$=\dfrac {a(a-1)+ab}{(a+b)(a+b-1)}=\dfrac {a(a+b-1)}{(a+b)(a+b-1)}=\dfrac {a}{a+b}$
设事件 A 表示第 2 个人取到白球，事件B1 表示第 1 个人取到白球，事件B2 表示第 1 个人取到红球。
步骤 2：应用全概率公式
根据全概率公式，我们有：
$P(A)=P(A|{B}_{1})P({B}_{1})+P(A|{B}_{2})P({B}_{2})$
步骤 3：计算条件概率
由于袋中有 a 只白球，b 只红球，所以：
$P({B}_{1})=\dfrac {a}{a+b}$
$P({B}_{2})=\dfrac {b}{a+b}$
当第 1 个人取到白球时，袋中还剩下 a-1 只白球和 b 只红球，所以：
$P(A|{B}_{1})=\dfrac {a-1}{a+b-1}$
当第 1 个人取到红球时，袋中还剩下 a 只白球和 b-1 只红球，所以：
$P(A|{B}_{2})=\dfrac {a}{a+b-1}$
步骤 4：代入全概率公式
将上述结果代入全概率公式中，得：
$P(A)=\dfrac {a-1}{a+b-1}\cdot \dfrac {a}{a+b}+\dfrac {a}{a+b-1}\cdot \dfrac {b}{a+b}$
$=\dfrac {a(a-1)+ab}{(a+b)(a+b-1)}=\dfrac {a(a+b-1)}{(a+b)(a+b-1)}=\dfrac {a}{a+b}$