题目
求lim _(xarrow 0)(dfrac (1+x)(1-{e)^-x}-dfrac (1)(x))。
求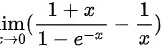 。
。
题目解答
答案
由题意可知,
对于本题给出的极限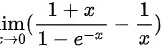 ,
,
经过观察,
我们容易发现,
该极限式子显然属于两个基本式子相减所组成的形式,
∴即可得,
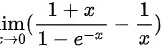
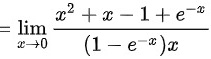
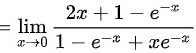
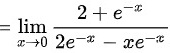
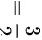
解析
考查要点:本题主要考查极限的计算,特别是处理复杂分式相减后的不定型(0/0型)问题,需要灵活运用洛必达法则或泰勒展开进行化简。
解题核心思路:
- 通分合并:将原式通分,转化为单一分式形式,观察是否形成0/0型不定式。
- 多次应用洛必达法则:对分子和分母分别求导,重复应用洛必达法则直至消除不定型。
- 代入求值:最终代入$x=0$计算极限值。
破题关键点:
- 识别不定型:通过通分发现分子分母均趋近于0,确定使用洛必达法则。
- 两次求导:需对分子分母各求导两次,确保消除所有不定型。
步骤1:通分合并表达式
原式为:
$\lim _{x\rightarrow 0}\left(\dfrac {1+x}{1-{e}^{-x}}-\dfrac {1}{x}\right)$
通分后得到:
$\lim _{x\rightarrow 0} \dfrac{(1+x)x - (1 - e^{-x})}{x(1 - e^{-x})}$
步骤2:验证0/0型不定式
当$x \rightarrow 0$时,分子为:
$x + x^2 - 1 + e^{-x} \approx 0 + 0 - 1 + 1 = 0$
分母为:
$x(1 - e^{-x}) \approx x \cdot x = x^2 \rightarrow 0$
因此属于0/0型不定式,可应用洛必达法则。
步骤3:第一次洛必达法则
对分子分母分别求导:
- 分子导数:$1 + 2x - e^{-x}$
- 分母导数:$(1 - e^{-x}) + x e^{-x}$
此时极限变为:
$\lim _{x\rightarrow 0} \dfrac{1 + 2x - e^{-x}}{1 - e^{-x} + x e^{-x}}$
步骤4:再次验证0/0型不定式
代入$x=0$,分子为$1 + 0 - 1 = 0$,分母为$0 + 0 = 0$,仍为0/0型,需再次应用洛必达法则。
步骤5:第二次洛必达法则
对分子分母再次求导:
- 分子导数:$2 + e^{-x}$
- 分母导数:$e^{-x} + e^{-x} - x e^{-x} = 2e^{-x} - x e^{-x}$
此时极限变为:
$\lim _{x\rightarrow 0} \dfrac{2 + e^{-x}}{2e^{-x} - x e^{-x}}$
步骤6:代入求值
将$x=0$代入得:
$\dfrac{2 + 1}{2 \cdot 1 - 0} = \dfrac{3}{2}$