函数=(x)^y在=(x)^y处的全微分=(x)^y______.
函数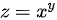 在
在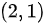 处的全微分
处的全微分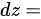 ______.
______.
题目解答
答案
已知函数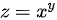 ,
,
则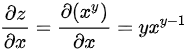 ,
,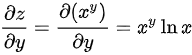 ,
,
所以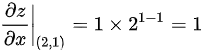 ,
,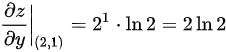 ,
,
故函数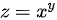 在
在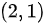 处的全微分
处的全微分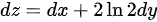 。
。
故答案为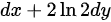 .
.
解析
考查要点:本题主要考查二元函数全微分的计算,涉及偏导数的求解及全微分公式的应用。
解题核心思路:
- 全微分公式:全微分$dz$由两个偏导数$\frac{\partial z}{\partial x}$和$\frac{\partial z}{\partial y}$与对应的变量变化$dx$、$dy$线性组合而成,即$dz = \frac{\partial z}{\partial x}dx + \frac{\partial z}{\partial y}dy$。
- 偏导数计算:
- 对$x$求偏导:将$y$视为常数,利用幂函数求导法则。
- 对$y$求偏导:将$x$视为常数,利用指数函数求导法则(需乘以$\ln x$)。
- 代入点$(2,1)$:将$x=2$,$y=1$代入偏导数表达式,得到具体数值。
破题关键:
- 正确应用求导规则:区分对$x$和$y$求导时的不同处理方式。
- 代入数值时的准确性:注意指数运算和对数运算的正确性。
步骤1:计算偏导数$\frac{\partial z}{\partial x}$
将$y$视为常数,对$x$求导:
$\frac{\partial z}{\partial x} = \frac{\partial}{\partial x} \left( x^y \right) = y x^{y-1}.$
步骤2:计算偏导数$\frac{\partial z}{\partial y}$
将$x$视为常数,对$y$求导:
$\frac{\partial z}{\partial y} = \frac{\partial}{\partial y} \left( x^y \right) = x^y \ln x.$
步骤3:代入点$(2,1)$
-
$\frac{\partial z}{\partial x}$在$(2,1)$处的值:
$\frac{\partial z}{\partial x} \bigg|_{(2,1)} = y x^{y-1} = 1 \cdot 2^{1-1} = 1 \cdot 2^0 = 1.$ -
$\frac{\partial z}{\partial y}$在$(2,1)$处的值:
$\frac{\partial z}{\partial y} \bigg|_{(2,1)} = x^y \ln x = 2^1 \cdot \ln 2 = 2 \ln 2.$
步骤4:构造全微分$dz$
将偏导数值代入全微分公式:
$dz = \frac{\partial z}{\partial x} dx + \frac{\partial z}{\partial y} dy = 1 \cdot dx + 2 \ln 2 \cdot dy = dx + 2 \ln 2 \, dy.$