题目
求曲线 =t-sin t, =1-cos t =4sin dfrac (t)(2) 在点 (dfrac (pi )(2)-1,1,2sqrt (2)) 处的切线及法平-|||-面方程.
题目解答
答案
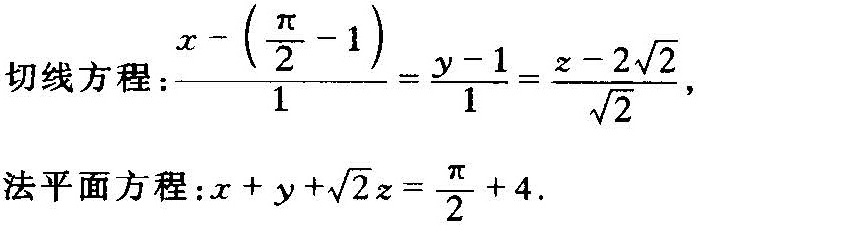
解析
步骤 1:确定参数 $t$ 的值
给定的点 $(\dfrac {\pi }{2}-1,1,2\sqrt {2})$ 在曲线上,因此我们需要找到对应的参数 $t$ 的值。根据 $x=t-\sin t$,$y=1-\cos t$,$z=4\sin \dfrac {t}{2}$,我们有:
$$
x = \dfrac {\pi }{2}-1 = t - \sin t
$$
$$
y = 1 = 1 - \cos t
$$
$$
z = 2\sqrt {2} = 4\sin \dfrac {t}{2}
$$
从 $y=1$ 可以直接得到 $\cos t = 0$,因此 $t = \dfrac {\pi }{2}$。将 $t = \dfrac {\pi }{2}$ 代入 $x$ 和 $z$ 的表达式中,可以验证它们也满足给定的点。
步骤 2:计算切线的方向向量
切线的方向向量由曲线的参数方程的导数给出。因此,我们需要计算 $x'(t)$,$y'(t)$ 和 $z'(t)$:
$$
x'(t) = 1 - \cos t
$$
$$
y'(t) = \sin t
$$
$$
z'(t) = 2\cos \dfrac {t}{2}
$$
将 $t = \dfrac {\pi }{2}$ 代入上述导数中,得到切线的方向向量:
$$
x'(\dfrac {\pi }{2}) = 1 - \cos \dfrac {\pi }{2} = 1
$$
$$
y'(\dfrac {\pi }{2}) = \sin \dfrac {\pi }{2} = 1
$$
$$
z'(\dfrac {\pi }{2}) = 2\cos \dfrac {\pi }{4} = \sqrt {2}
$$
因此,切线的方向向量为 $(1, 1, \sqrt {2})$。
步骤 3:写出切线方程
切线方程可以表示为:
$$
\dfrac {x - x_0}{x'(t)} = \dfrac {y - y_0}{y'(t)} = \dfrac {z - z_0}{z'(t)}
$$
其中 $(x_0, y_0, z_0)$ 是给定点 $(\dfrac {\pi }{2}-1,1,2\sqrt {2})$。将方向向量和给定点代入,得到切线方程:
$$
\dfrac {x - (\dfrac {\pi }{2}-1)}{1} = \dfrac {y - 1}{1} = \dfrac {z - 2\sqrt {2}}{\sqrt {2}}
$$
简化得到:
$$
x - \dfrac {\pi }{2} + 1 = y - 1 = \dfrac {z - 2\sqrt {2}}{\sqrt {2}}
$$
步骤 4:写出法平面方程
法平面方程可以表示为:
$$
(x - x_0)x'(t) + (y - y_0)y'(t) + (z - z_0)z'(t) = 0
$$
将方向向量和给定点代入,得到法平面方程:
$$
(x - (\dfrac {\pi }{2}-1)) \cdot 1 + (y - 1) \cdot 1 + (z - 2\sqrt {2}) \cdot \sqrt {2} = 0
$$
简化得到:
$$
x + y + \sqrt {2}z = \dfrac {\pi }{2} + 4
$$
给定的点 $(\dfrac {\pi }{2}-1,1,2\sqrt {2})$ 在曲线上,因此我们需要找到对应的参数 $t$ 的值。根据 $x=t-\sin t$,$y=1-\cos t$,$z=4\sin \dfrac {t}{2}$,我们有:
$$
x = \dfrac {\pi }{2}-1 = t - \sin t
$$
$$
y = 1 = 1 - \cos t
$$
$$
z = 2\sqrt {2} = 4\sin \dfrac {t}{2}
$$
从 $y=1$ 可以直接得到 $\cos t = 0$,因此 $t = \dfrac {\pi }{2}$。将 $t = \dfrac {\pi }{2}$ 代入 $x$ 和 $z$ 的表达式中,可以验证它们也满足给定的点。
步骤 2:计算切线的方向向量
切线的方向向量由曲线的参数方程的导数给出。因此,我们需要计算 $x'(t)$,$y'(t)$ 和 $z'(t)$:
$$
x'(t) = 1 - \cos t
$$
$$
y'(t) = \sin t
$$
$$
z'(t) = 2\cos \dfrac {t}{2}
$$
将 $t = \dfrac {\pi }{2}$ 代入上述导数中,得到切线的方向向量:
$$
x'(\dfrac {\pi }{2}) = 1 - \cos \dfrac {\pi }{2} = 1
$$
$$
y'(\dfrac {\pi }{2}) = \sin \dfrac {\pi }{2} = 1
$$
$$
z'(\dfrac {\pi }{2}) = 2\cos \dfrac {\pi }{4} = \sqrt {2}
$$
因此,切线的方向向量为 $(1, 1, \sqrt {2})$。
步骤 3:写出切线方程
切线方程可以表示为:
$$
\dfrac {x - x_0}{x'(t)} = \dfrac {y - y_0}{y'(t)} = \dfrac {z - z_0}{z'(t)}
$$
其中 $(x_0, y_0, z_0)$ 是给定点 $(\dfrac {\pi }{2}-1,1,2\sqrt {2})$。将方向向量和给定点代入,得到切线方程:
$$
\dfrac {x - (\dfrac {\pi }{2}-1)}{1} = \dfrac {y - 1}{1} = \dfrac {z - 2\sqrt {2}}{\sqrt {2}}
$$
简化得到:
$$
x - \dfrac {\pi }{2} + 1 = y - 1 = \dfrac {z - 2\sqrt {2}}{\sqrt {2}}
$$
步骤 4:写出法平面方程
法平面方程可以表示为:
$$
(x - x_0)x'(t) + (y - y_0)y'(t) + (z - z_0)z'(t) = 0
$$
将方向向量和给定点代入,得到法平面方程:
$$
(x - (\dfrac {\pi }{2}-1)) \cdot 1 + (y - 1) \cdot 1 + (z - 2\sqrt {2}) \cdot \sqrt {2} = 0
$$
简化得到:
$$
x + y + \sqrt {2}z = \dfrac {\pi }{2} + 4
$$